Geometrie im Raum. Gegenseitige Anordnung zweier Ebenen im Raum Zeichen der Parallelität zweier Ebenen

Die Beziehung der Parallelität von Ebenen, ihre Eigenschaften und Anwendungen werden betrachtet.

Eine visuelle Darstellung des Standorts von zwei

Flugzeuge gibt Modellierung mit Ebenen von Oberflächen benachbarter Wände, der Decke und des Bodens eines Raums, Etagenbetten, zwei befestigten Blättern Papier

Zauberer usw. (Abb. 242-244).

Obwohl es unendlich viele Möglichkeiten für die relative Lage verschiedener Ebenen gibt, zu deren Festlegung und Charakterisierung später Winkel- und Abstandsmessungen verwendet werden, werden wir uns zunächst mit denen befassen, bei denen die Klassifizierung (sowie Linien mit Ebenen) basiert auf der Anzahl ihrer gemeinsamen Punkte.

1. Zwei Ebenen haben mindestens drei gemeinsame Punkte, die nicht auf derselben Geraden liegen. Solche Ebenen fallen zusammen (Axiom C 2 , §7).

2. Gemeinsame Punkte zweier Ebenen liegen auf einer Geraden, die die Schnittlinie dieser Ebenen ist (Axiom C 3, § 7). Solche Ebenen schneiden sich.

3. Die beiden Ebenen haben keine gemeinsamen Punkte.

BEI in diesem Fall werden sie aufgerufen parallel-

Zwei Ebenen heißen parallel, wenn sie keine gemeinsamen Punkte haben.

Die Parallelität von Ebenen wird mit || bezeichnet: α || β.

Wie immer bei der Vorstellung geometrische Konzepte entstand-

Es gibt ein Problem mit ihrer Existenz. Die Existenz von Kreuz-

Flugzeuge ist Kennzeichen Platz,

und wir haben es schon oft benutzt. Weniger offensichtlich

die Existenz paralleler Ebenen. Es gibt kein

bezweifelt, dass zum Beispiel die Ebenen der gegenüberliegenden Gesichter

Würfel sind parallel dazu, das heißt, sie schneiden sich nicht. Aber sofort

Per Definition ist es sicherlich unmöglich, dies festzustellen. Zum Lösen

die aufgeworfene Frage, sowie andere damit zusammenhängende Fragen

Parallelität der Ebenen, ist es notwendig, ein Parallelitätszeichen zu haben.

Um nach einem Zeichen zu suchen, ist es ratsam, das Flugzeug zu betrachten,

aus geraden Linien „gewebt“. Offensichtlich ist jede Zeile einer von

Parallele Ebenen müssen parallel zueinander sein.

Andernfalls haben die Ebenen einen gemeinsamen Punkt. Dosta-

Sind die Parallelitäten der Ebene β genau zu einer geraden Ebene α

dass die Ebenen α und β parallel sind? Bedingungslos

aber nein (begründe es!). Praktische Erfahrung bezeugt das

zwei solcher Schnittlinien sind ausreichend. Anheften

Auf dem Mast eine Plattform parallel zum Boden, es reicht aus, sie zu stellen

parallel zur zweiten Ebene sind, dann sind diese Ebenen parallel.

 Die Schnittlinien a und b der Ebene α seien parallel zur Ebene β. Beweisen wir, dass die Ebenen α und β parallel sind durch Widerspruch. Dazu nehmen wir an, dass sich die Ebenen α und β entlang der Geraden schneiden

t (Abb. 246). Die Linien a und b können nach Annahme keine geraden Linien schneiden. Dann aber werden in der Ebene α zwei Geraden durch einen Punkt gezogen, die die Gerade m nicht schneiden, also parallel zu ihr verlaufen. Es ist ein Widerspruch

und vervollständigt den Beweis des Satzes.

Das Zeichen der Parallelität der Ebenen wird für die horizontale Platzierung von flachen Strukturen (Betonplatten, Böden, Scheibengoniometer usw.) unter Verwendung von zwei Ebenen verwendet, die in der Ebene der Struktur auf sich schneidenden Linien angeordnet sind. Basierend auf dieser Funktion können Sie eine Ebene parallel zu der angegebenen erstellen.

Aufgabe 1. Zeichne durch einen Punkt, der außerhalb der gegebenen Ebene liegt, eine Ebene parallel zu der gegebenen.

 Die Ebene β und der Punkt M seien außerhalb der Ebene gegeben (Abb. 247, a). Zeichnen wir durch den Punkt M zwei sich schneidende Geraden a und b parallel zur Ebene β. Dazu müssen Sie in der Ebene β zwei sich schneidende Linien c und d nehmen (Abb. 247, b). Zeichnen Sie dann durch Punkt M gerade Linien a und b, parallel zu den geraden Linien c bzw. d.

aber (Abb. 247, c).

Schnittlinien a und b parallel zur Ebene β sind, nach dem Kriterium der Parallelität der Linie und der Ebene (Theorem 1 §11). Sie definieren eindeutig die Ebene α. Nach dem bewährten Kriterium ist α || β.

Beispiel 1. Würfel ABCDA 1 B 1 C 1 D 1 ist gegeben, die Punkte M, N, P sind die Mittelpunkte der Kanten BC, B 1 C 1 bzw. A 1 D 1. Installieren gegenseitiges Einverständnis Flugzeuge: 1) ABB 1 und PNM; 2) NMA und A 1 C 1 C; 3) A 1 NM

und PC 1 C; 4) MAD 1 und DB 1 C.

 1) Die Ebenen ABB 1 und РNM (Abb. 248) sind parallel, aufgrund der Parallelität der Ebenen (Satz 1). Tatsächlich schneiden sich die Linien PN und NM und sind parallel zu der Ebene ABB 1, aufgrund der Parallelität der Linie und der Ebene (Theorem 1 § 11), weil die Segmente PN und NM die Mittelpunkte der gegenüberliegenden Seiten verbinden die Quadrate, also sind sie parallel zu den Seiten der Quadrate:

PN ||A 1 B 1 ,NM ||B 1 B.

2) Die Ebenen NMA und A 1 C 1 C schneiden sich entlang der Geraden AA 1 (Abb. 249). Tatsächlich sind die Linien AA 1 und CC 1 aufgrund der Parallelität der Linien parallel (AA 1 ||ВB 1 ,ВB 1 ||СC 1 ). Daher liegt die Gerade AA 1 in der Ebene A 1 C 1 C . In ähnlicher Weise wird die Zugehörigkeit der Geraden AA 1 zur Ebene NMA begründet.

3) Die Ebenen A 1 NM und PC 1 C (Abb. 250) sind parallel, aufgrund der Parallelität der Ebenen. Tatsächlich ist NM ||С 1 C . Daher ist die Linie NM parallel zur Ebene PC 1 C. Die Segmente PC 1 und A 1 N sind ebenfalls parallel, da das Viereck PC 1 NA 1 ein Parallelogramm ist (A 1 P ||NC 1 ,A 1 P = NC 1). Somit ist die Linie A 1 N parallel zur Ebene PC 1 C. Die Linien A 1 N und NM schneiden sich.

4) Die Ebenen MAD 1 und DB 1 C schneiden sich (Abb. 251). Obwohl es nicht einfach ist, eine Linie ihres Schnittpunkts zu ziehen, ist es nicht schwierig, einen Punkt dieser Linie anzugeben. Tatsächlich sind die Geraden A 1 D und B 1 C parallel, da das Viereck A 1 B 1 CD ein Parallelogramm ist (A 1 B 1 = AB = CD ,A 1 B 1 ||AB ,AB ||CD ). Daher gehört die Linie A 1 D zur Ebene DB 1 C. Die Linien A 1 D und AD 1 schneiden sich in einem gemeinsamen Punkt der Ebenen MAD 1 und DB 1 C.

Wenn zwei sich schneidende Geraden einer Ebene jeweils parallel zu zwei Geraden einer anderen Ebene sind, dann sind diese Ebenen parallel.

Unter Verwendung des Parallelitätszeichens einer Geraden und einer Ebene (Satz 1 §11) lässt sich leicht feststellen, dass die Bedingung von Satz 1 aus der Bedingung von Satz 1′ folgt.

Natürlich stellt sich die Frage nach der Eindeutigkeit der in Aufgabe 1 angegebenen Konstruktion. Da wir diese Eigenschaft mehr als einmal verwenden müssen, trennen wir sie als separaten Satz. Betrachten Sie jedoch zunächst eine andere Aussage.

Satz 2 (über den Schnitt zweier paralleler Ebenen mit einer dritten).

Wenn zwei parallele Ebenen von einer dritten Ebene geschnitten werden, dann sind die Schnittlinien der Ebenen parallel.

 Gegeben seien die parallelen Ebenen α, β und die sie schneidende Ebene γ (Abb. 252). Bezeichne die Schnittlinien

durch a und b. Diese Linien liegen in der Ebene γ und schneiden sich nicht, da die Ebenen α und β keine gemeinsamen Punkte haben. Daher direkt

meine a und b sind parallel.

Satz 3 (über die Existenz und Eindeutigkeit einer Ebene parallel zu einer gegebenen).

Durch einen Punkt außerhalb einer gegebenen Ebene gibt es nur eine Ebene parallel zu der gegebenen Ebene.

 Die Konstruktion eines solchen Flugzeugs wird in Aufgabe 1 durchgeführt. Wir werden die Eindeutigkeit der Konstruktion durch Widerspruch beweisen. Nehmen wir an, durch den Punkt M würden zwei verschiedene Ebenen α und γ gezogen, pa-

parallele Ebenen β (Abb. 253), und die gerade Linie m ist die Linie ihrer Schnittlinie. Zeichnen wir durch den Punkt M die Ebene δ, die die Gerade schneidet

m und Ebene β (wie geht das?). Bezeichnen Sie mit und b

die Schnittlinie der Ebene δ mit den Ebenen α und γ und durch die Schnittlinie der Ebenen δ und β (Abb. 253). Nach Satz 2 gilt a ||c

und b || c. Das heißt, in der δ-Ebene hindurch

Der Punkt M wird von zwei Geraden parallel zu Geraden passiert. Der Widerspruch weist auf die Unrichtigkeit der Annahme hin.

Die Beziehung der Parallelität von Ebenen hat eine Reihe von Eigenschaften, die Analoga in der Planimetrie haben.

Satz 4 (über Segmente paralleler Geraden zwischen parallelen Ebenen).

Segmente paralleler Linien, die von parallelen Ebenen abgeschnitten werden, sind einander gleich.

 Seien zwei parallele Ebenen α und β und Segmente AB

und CD parallele Linien a und d, abgeschnitten von diesen Ebenen (Abb. 254, a). Zeichnen wir die Ebene γ durch die Linien a und d (Abb. 254, b). Sie schneidet die Ebenen α und β entlang der Linien AC und BD, die nach Theorem 2 parallel sind. Daher ist das Viereck ABCD ein Parallelogramm, seine gegenüberliegenden Seiten AC und BD sind gleich.

Aus der obigen Eigenschaft folgt, dass wenn wir von allen Punkten der Ebene absehen

eine Seite des Flugzeugs parallele Segmente gleich lang, dann bilden die Enden dieser Segmente zwei parallele Ebenen. Auf dieser Eigenschaft beruht die Konstruktion eines Quaders durch Ablagerung von Segmenten (Abb. 255).

Satz 5 (über die Transitivität des Parallelitätsverhältnisses von Ebenen).

Wenn jede der beiden Ebenen parallel zur dritten ist, dann sind diese beiden Ebenen parallel zueinander.

 Die Ebenen α und β seien parallel zur Ebene γ. Nehmen wir das an

α und β sind nicht parallel. Dann haben die Ebenen α und β einen gemeinsamen Punkt, und zwei verschiedene Ebenen gehen durch diesen Punkt und sind parallel zur Ebene γ, was Satz 3 widerspricht. Daher haben die Ebenen α und β keine gemeinsamen Punkte, das heißt, sie sind es parallel.

Satz 5 ist ein weiteres Zeichen für die Parallelität von Ebenen. Es ist sowohl in der Geometrie als auch in der Geometrie weit verbreitet praktische Tätigkeiten. Beispielsweise garantiert in einem mehrstöckigen Gebäude die Parallelität der Boden- und Deckenebenen auf jedem Stockwerk deren Parallelität auf verschiedenen Stockwerken.

Aufgabe 2. Beweisen Sie: Wenn eine Gerade a die Ebene α schneidet, dann schneidet sie auch jede Ebene parallel zur Ebene α.

 Die Ebenen α und β seien parallel, und die Gerade a schneide die Ebene α im Punkt A. Beweisen wir, dass sie auch die Ebene schneidet

β. Nehmen wir an, dass dies nicht der Fall ist. Dann ist die Linie a parallel zur Ebene β. Ziehen wir die Ebene γ durch die Gerade a und einen beliebigen Punkt der Ebene β (Abb. 256).

Diese Ebene schneidet parallele Ebenen α und β entlang gerader Linien b und . Co-

nach Theorem 2, b || c, d.h. in der Ebene γ durch den Punkt A verlaufen zwei Geraden a und b parallel zur Geraden c . Dieser Widerspruch beweist die Behauptung.

Versuchen Sie selbst zu beweisen, dass, wenn eine Ebene α eine Ebene β schneidet, sie auch jede Ebene parallel zur Ebene β schneidet.

Beispiel 2. Im Tetraeder ABCD sind die Punkte K, F, E die Mittelpunkte der Kanten DA, DC, DB, aM und P sind die Massenschwerpunkte der Flächen ABD bzw. BCD.

1) Stellen Sie die relative Position der KEF- und ABC-Ebenen ein;

DEF und ABC.

2) Konstruieren Sie die Schnittlinie der Ebenen AFB und KEC.

3) Finden Sie die Querschnittsfläche des Tetraeders durch eine Ebene parallel zur Ebene ABD und durch den Punkt P, wenn alle Kanten des Tetraeders gleich sind.

 Lassen Sie uns ein Bild erstellen, das der Bedingung entspricht (Abb. 257, a). 1) Die Ebenen KEF und ABC sind parallel, aufgrund der Parallelität der Ebenen (Satz 1'): Die Schnittgeraden KE und KF der Ebene KEF sind parallel zu den Schnittgeraden AB und AC der Ebene ABC (die Mittellinien der entsprechenden

Dreiecke zeichnen).

Die Ebenen DEF und ABC schneiden sich entlang der Linie BC, da die Linie BC zu beiden Ebenen gehört und sie nicht zusammenfallen können - die Punkte A, B, C, D liegen nicht in derselben Ebene.

2) Die Ebene AFB schneidet die Ebene KEC entlang einer den Punkt P enthaltenden Geraden, da die in diesen Ebenen liegenden Linien CE und BF in der Ebene BCD liegen und sich im Punkt P schneiden. Ein weiterer Punkt ist der Schnittpunkt der Q-Linien AF und CK in der Ebene ACD (Abb. 257, b). Offensichtlich ist dieser Punkt der Schwerpunkt der ACD-Fläche. Der gewünschte Schnittpunkt ist die Linie PQ.

3) Bauen wir den in der Bedingung angegebenen Schnitt unter Verwendung des Zeichens der Parallelität der Ebenen. Lassen Sie uns Linien durch die Punkte P und Q parallel zu den Linien DB bzw. DA ziehen (Abb. 257, c). Diese Linien schneiden das Segment CD am Punkt L. Letzteres folgt aus der Eigenschaft des Massenschwerpunkts eines Dreiecks - es teilt die Seitenhalbierenden des Dreiecks im Verhältnis 2: 1, von oben gezählt. Es bleibt der Satz von Thales anzuwenden. Somit sind die Ebenen PLQ und BDA parallel. Der gewünschte Abschnitt ist das Dreieck LSN.

Konstruktionsbedingt sind die Dreiecke BCD und SCL ähnlich mit dem Ähnlichkeitskoeffizienten CE CP =3 2 . Daher ist LS = 3 2 BD . Ebenso die

Gleichheiten werden hinzugefügt: LN =3 2 AD ,NS =3 2 AB . Dies impliziert, dass die Dreiecke LSN und ABD mit dem Ähnlichkeitskoeffizienten 3 2 ähnlich sind. Durch die Eigenschaften der Flächen ähnlicher Dreiecke,

S LNS =4 9 S ABD . Es bleibt die Fläche des Dreiecks ABD zu finden. Durch-

da alle Kanten des Tetraeders bedingt gleich a sind, dann ist S ABD =4 3 a 2 .

Der gewünschte Bereich ist 3 1 3 a 2 .

Es ist angebracht, darauf zu achten, dass die Antwort nur von der Fläche der Facette ABD abhängt. Daher ist die Gleichheit aller Kanten nur ein Mittel, um diesen Bereich zu finden. Somit kann dieses Problem im Wesentlichen verallgemeinert werden.

Antworten. 1)KEF ||ABC ; 3)3 1 3 ein 2 .

 Kontrollfragen

1. Ist es wahr, dass zwei Ebenen parallel sind, wenn jede Linie in einer Ebene parallel zur anderen Ebene ist?

2. Die Ebenen α und β sind parallel. Liegen Schnittlinien in diesen Ebenen?

3. Zwei Seiten eines Dreiecks sind parallel zu einer Ebene. Ist die dritte Seite des Dreiecks parallel zu dieser Ebene?

4. Zwei Seiten eines Parallelogramms sind parallel zu einer Ebene. Stimmt es, dass die Ebene des Parallelogramms parallel zur gegebenen Ebene ist?

5. Können die Segmente zweier gerader Linien, die von parallelen Ebenen abgeschnitten werden, ungleich sein?

6. Kann der Querschnitt eines Würfels ein gleichschenkliges Trapez sein? Kann der Querschnitt eines Würfels ein regelmäßiges Fünfeck sein? Stimmt es, dass zwei Ebenen parallel zu derselben Linie parallel zueinander sind?

Die Schnittlinien der Ebenen α und β mit der Ebene γ sind parallel zueinander. Sind die Ebenen α und β parallel?

Können drei Seiten eines Würfels parallel zu derselben Ebene sein?

Grafische Übungen

1. Abbildung 258 zeigt einen Würfel ABCDA 1 B 1 C 1 D 1 , die Punkte M , N , K , L , P sind die Mittelpunkte der entsprechenden Kanten. Füllen Sie die Tabelle gemäß dem gegebenen Muster aus und wählen Sie die gewünschte Anordnung der Ebenen α und β.

Gegenseitig

Lage

α || β α = β

α × β α || β α = β

2. In Abb. 259 zeigt das Tetraeder ABCD, die Punkte K, F, M, N, Q sind die Mittelpunkte der entsprechenden Kanten. Angeben:

1) eine Ebene, die durch den Punkt K parallel zur Ebene ABC verläuft;

2) eine Ebene, die durch die Linie BD parallel zur Ebene MNQ verläuft.

3. Bestimmen Sie den Schnitt der Figur durch eine Ebene, die durch die drei in der Figur gezeigten Punkte verläuft.

kah 260, a)–e) und 261, a)–d).

4. Erstellen Sie eine Zeichnung gemäß den angegebenen Daten.

1) Von den Scheitelpunkten des Parallelogramms ABCD, die in einer der beiden parallelen Ebenen liegen, werden parallele Linien gezogen, die die zweite Ebene jeweils in den Punkten A 1 , B 1 , C 1 , D 1 schneiden.

2) Das Dreieck A 1 B 1 C 1 ist die Projektion des Dreiecks ABC auf die dazu parallele Ebene α. Punkt M ist die Mitte des BC, M 1 ist die Projektion des Punktes M auf die Ebene α.

207. Im Würfel ABCDA 1 B 1 C 1 D 1 sind die Punkte O, O 1 die Mittelpunkte der Flächen ABCD bzw. A 1 B 1 C 1 D 1, M ist die Mitte der Kante AB.

1°) Bestimmen Sie die relative Position der Ebenen MO 1 O

und ADD 1 , ABD 1 und CO 1 C 1 .

2°) Konstruiere den Schnittpunkt der Ebene DCC 1 und der Linie MO 1 und die Schnittlinie der Ebenen MCC 1 und A 1 D 1 C 1 .

3) Finden Sie die Querschnittsfläche des Würfels durch eine Ebene, die parallel zur Ebene AD 1 C 1 ist und durch den Punkt O 1 geht, wenn die Kante des Würfels gleich a ist.

208. Im Tetraeder ABCD sind die Punkte K , L , P die Massenschwerpunkte der Flächen ABD , BDC , ABC bzw. aM ist der Mittelpunkt der Kante AD .

1°) Bestimmen Sie die relative Position der ACD-Ebenen

und KLP , MLK und ABC .

2°) Konstruieren Sie den Schnittpunkt der Ebene ABC mit der Linie ML und die Schnittlinie der Ebenen MKL und ABC.

3) Finden Sie die Querschnittsfläche des Tetraeders durch eine Ebene, die durch die Punkte K, L und M parallel zur geraden Linie AD verläuft, wenn alle Kanten des Tetraeders gleich sind.

209. Würfel ABCDA 1 B 1 C 1 D 1 ist gegeben. Die Punkte L, M, M 1 sind die Mittelpunkte der Kanten AB, AD bzw. A 1 D 1 .

1°) Bestimmen Sie die relative Position der Ebenen B 1 D 1 D

und LMM1.

2) Konstruiere eine Ebene, die durch den Punkt M parallel zur Ebene ACC 1 geht.

3) Konstruieren Sie einen Schnitt des Würfels durch eine Ebene, die durch den Punkt M 1 parallel zur Ebene CDD 1 verläuft.

4) Bestimmen Sie die relative Position der Ebenen MA 1 IN 1

und CDM1.

5) Konstruieren Sie eine Ebene, die durch die Linie C 1 D 1 parallel zur Ebene CDM 1 verläuft.

210. In einer regulären viereckigen Pyramide SABCD sind alle Kanten einander gleich. Die Punkte L, M und N sind jeweils die Mittelpunkte der Kanten AS, BS, CS.

1°) Bestimmen Sie die relative Position von: geraden Linien LM und BC; Gerade LN und Ebene ABD; Flugzeuge LMN und BDC.

2°) Beweisen Sie, dass die Dreiecke ABC und LMN ähnlich sind.

3) Konstruieren Sie einen Abschnitt der Pyramide durch die Ebene AMN ; Ebene LMN; Flugzeug LBC.

4*) Welcher der durch die Spitze S verlaufenden Pyramidenabschnitte hat die größte Fläche?

Parallelität von Linien und Ebenen

Im SABC-Tetraeder sind alle Flächen regelmäßige Dreiecke. Die Punkte L, M und N sind jeweils die Mittelpunkte der Kanten AS, BS, CS. 1°) Bestimmen Sie die relative Position der Linien LM und BC. 2°) Bestimmen Sie die relative Lage der Geraden LN und der Ebene ABC.

3) Beweisen Sie, dass die Dreiecke LMN und ABC ähnlich sind.

Konstruieren Sie einen Abschnitt eines Würfels, der ist: 1°) ein gleichseitiges Dreieck; 2) ein Fünfeck.

217. Konstruieren Sie einen Abschnitt eines Tetraeders, der ein Parallelogramm ist.

218°. Beweisen Sie, dass die gegenüberliegenden Flächen des Parallelepipeds parallel sind.

219. Beweisen Sie, dass die Menge aller Geraden, die durch einen gegebenen Punkt und parallel zu einer gegebenen Ebene verlaufen, eine Ebene bildet, die parallel zu der gegebenen ist.

220. Gegeben vier Punkte A , B , C , D , die nicht in derselben Ebene liegen. Beweisen Sie, dass jede Ebene parallel zu den Linien AB und CD die Linien AC, AD, BD, BC an den Ecken des Parallelogramms schneidet.

221. Beweisen Sie, dass eine Ebene und eine Linie, die nicht zu dieser Ebene gehört, parallel zueinander sind, wenn sie beide parallel zu derselben Ebene sind.

222. Eine Ebene wird durch den Schnittpunkt O der Diagonalen des Würfels ABCDA 1 B 1 C 1 D 1 parallel zur Fläche ABCD gezogen. Diese Ebene schneidet die Kanten BB 1 und CC 1 an den Punkten M bzw. N. Beweisen Sie, dass der Winkel MON ein rechter Winkel ist.

223. Beweisen Sie, dass zwei Ebenen genau dann parallel zueinander sind, wenn jede Gerade, die eine der Ebenen schneidet, die andere schneidet.

224*. Zeichnen Sie in der dreieckigen Pyramide SABC durch die Segmente AD und CE, wobei D die Mitte von SB und E die Mitte von SA ist, Abschnitte der Pyramide parallel zueinander.

225. Finden Sie geometrische Orte:

1) die Mittelpunkte aller Segmente mit Enden auf zwei gegeben parallele Ebenen; 2*) Mittelpunkte von Segmenten, deren Enden auf zwei gegebenen Schnittlinien liegen.

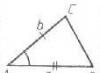
226*. Die in der Ebene α liegende Seite AB des Dreiecks ABC ist parallel zur Ebene β. Ein gleichseitiges Dreieck A 1 B 1 C 1 ist eine Parallelprojektion des Dreiecks ABC auf die Ebene β; AB \u003d 5, BC \u003d 6, AC \u003d 9.

1) Stellen Sie die relative Position der geraden Linien AB und A 1 B 1 ein,

BC und B1 C1 , A1 C1 und AC.

2) Finden Sie die Fläche des Dreiecks A 1 B 1 C 1.

227*. Gegeben seien zwei sich schneidende Geraden. Geben Sie die Menge aller Punkte im Raum an, durch die es möglich ist, eine Linie zu ziehen, die jede der beiden gegebenen Linien schneidet.

Grundlegende Definition

Die beiden Flugzeuge werden aufgerufen

sind parallel,

wenn sie keine gemeinsamen Punkte haben.

Hauptaussagen

Zeichen der Parallelität Wenn zwei sich schneidende Geraden einer Ebene einer Ebene jeweils parallel zu zwei Geraden der zweiten Ebene sind, dann sind diese Ebenen

Knochen sind parallel.

Der ne-parallele Satz Wenn zwei parallele Schnitte zweier ne-paralleler Ebenen von einer dritten Ebene geschnitten werden, dann ist die

die sind parallel.

a α,b α,a ×b ,c β,d β,a ||c ,b ||d α || β

α || β, a = γ∩α,b = γ∩βa ||b

Ma

β: α || β,M β

Vorbereitung für thematische

an wen Gutachten zum Thema „Parallelität von Linien und Flächen“

Aufgaben zur Selbstkontrolle

1. Die vier Punkte gehören nicht zur selben Ebene. Können etwa drei von ihnen auf derselben Linie liegen?

2. Können drei verschiedene Ebenen genau zwei Punkte gemeinsam haben?

3. Können zwei sich schneidende Geraden gleichzeitig parallel zu einer dritten Geraden sein?

4. Stimmt das so gerade a und b sind nicht parallel, wenn es keine Gerade c parallel zu a und b gibt?

5. Können gleiche Segmente ungleiche Projektionen haben?

6. Kann ein Strahl eine Parallelprojektion einer Linie sein?

7. Kann ein Quadrat ein Bild eines Würfels sein?

8. Stimmt es, dass es durch einen gegebenen Punkt im Raum nur eine Ebene parallel zu einer gegebenen Geraden geben kann?

9. Ist es immer möglich, eine Linie durch einen gegebenen Punkt parallel zu zwei gegebenen Ebenen zu ziehen, die diesen Punkt nicht enthalten?

10. Kann man durch zwei sich schneidende Geraden parallele Ebenen zeichnen?

Antworten auf Aufgaben zur Selbstkontrolle

Testprobe

Zwei Parallelogramme ABCD und ABC 1 D 1 liegen in verschiedenen Ebenen.

1°) Bestimmen Sie die relative Position der Linien CD und C 1 D 1 .

2°) Bestimmen Sie die relative Position der Linie C 1 D 1 und der Ebene

3°) Konstruiere eine Schnittlinie der Ebenen DD 1 C 1 und BCC 1 .

4 °) Bestimmen Sie die relative Position der Ebenen ADD 1 und BCC 1.

5) Zeichnen Sie durch den Punkt M, indem Sie das Segment AB im Verhältnis 2: 1 teilen und von Punkt A aus zählen, eine Ebene α parallel zur Ebene C 1 BC. 6) Konstruiere den Schnittpunkt der Geraden AC mit der Ebene α und finde das Verhältnis, in dem dieser Punkt die Strecke AC teilt.

Gegenseitige Anordnung von Geraden und Ebenen im Raum

Trigonometrisch

Sie haben sich bereits im Geometrieunterricht mit trigonometrischen Funktionen auseinandergesetzt. Bisher beschränkten sich ihre Anwendungen hauptsächlich auf die Lösung von Dreiecken, das heißt, es ging darum, einige Elemente eines Dreiecks aus anderen zu finden. Aus der Geschichte der Mathematik ist bekannt, dass die Entstehung der Trigonometrie mit der Messung von Längen und Winkeln verbunden ist. Doch jetzt der Umfang

Sie Die Anwendungen sind viel breiter als in der Antike.

Das Wort Trigonometrie kommt aus dem Griechischen τριγωνον

(trigonon) - ein Dreieck und µετρεω (metreo) - ich messe, ändere

ryu. Wörtlich bedeutet es die Messung von Dreiecken.

BEI Dieses Kapitel systematisiert den Ihnen bereits bekannten Stoff aus dem Studium der Geometrie, das Studium geht weiter trigonometrische Funktionen und ihre Anwendungen zu charakterisieren periodische Prozesse, insbesondere Rotationsbewegungen, Schwingungsvorgänge usw.

Die meisten Anwendungen der Trigonometrie betreffen genau periodische Prozesse, also Prozesse, die sich in regelmäßigen Abständen wiederholen. Der Aufgang und Untergang der Sonne, der Wechsel der Jahreszeiten, das Drehen des Rades sind die einfachsten Beispiele für solche Vorgänge. Auch mechanische und elektromagnetische Schwingungen sind wichtige Beispiele für periodische Prozesse. Daher ist die Untersuchung periodischer Prozesse eine wichtige Aufgabe. Und die Rolle der Mathematik bei ihrer Lösung ist entscheidend.

Vorbereitung auf das Studium des Themas "Trigonometrische Funktionen"

Es ist ratsam, mit dem Studium des Themas "Trigonometrische Funktionen" zu beginnen, indem die Definitionen und Eigenschaften der trigonometrischen Funktionen der Winkel von Dreiecken und ihre Anwendungen zum Lösen sowohl rechtwinkliger als auch beliebiger Dreiecke wiederholt werden.

Sinus, Cosinus, Tangens, Winkelkotangens eines Rechtecks

Dreieck

Tabelle 24

Der Sinus eines spitzen Winkels ist das Verhältnis des gegenüberliegenden Beins zur Hypotenuse:

sinα = a c .

Der Kosinus eines spitzen Winkels ist das Verhältnis des angrenzenden Schenkels zur Hypotenuse:

cosα = b c .

Die Tangente eines spitzen Winkels ist das Verhältnis des gegenüberliegenden Schenkels zum benachbarten:

tgα = a b .

Der Kotangens eines spitzen Winkels ist das Verhältnis des benachbarten Schenkels zum gegenüberliegenden:

ctga = ein b .

Sinus, Kosinus, Tangens, Kotangens von Winkeln von 0° bis 180°

Tabelle 25

sin α = R y ; cosα = R x ;

tgα = x y ; ctga = x j.

(X;bei) - Punktkoordinaten ABER befindet sich im oberen Halbkreis, α - der durch den Radius gebildete Winkel OA Kreis mit Achse X.

Sinus-, Kosinus-, Tangens-, Kotangens-Werte

einige Ecken

Tabelle 26

Ecke t

Beliebige Dreiecke lösen

Tabelle 27

Sinussatz

Die Seiten eines Dreiecks sind proportional zu den Sinus der gegenüberliegenden Winkel:

Sünde aα = Sünde bβ = Sünde cγ .

Kosinussatz

Das Quadrat einer beliebigen Seite eines Dreiecks ist gleich der Summe der Quadrate der beiden anderen Seiten, ohne das Produkt dieser Seiten mit dem Kosinus des Winkels zwischen ihnen zu verdoppeln:

c2 = a2 + b2 − 2 ab cos γ ,b2 = a2 + c2 − 2 ac cos β , a2 = b2 + c2 − 2 v. Chr cos α .

Die Fläche eines Dreiecks ist die Hälfte des Produkts seiner beiden Seiten und des Sinus des Winkels zwischen ihnen:

S=1 2 abSündeγ = 1 2 acSündeβ = 1 2 v. ChrSündeα .

Grundlegende trigonometrische Identitäten

5. Vergleichen Sie die Summe der Sinus der spitzen Winkel eines beliebigen rechtwinkligen Dreiecks (wir bezeichnen es mitABER) mit Einheit.

< 1. B.ABER= 1.

> 1. G. Es ist unmöglich zu vergleichen. Aufsteigend sortieren: a= sin 30°, b= cos 30°,

= TG 30°.

< b<c.B.a<c<b

15. Punktkoordinaten angebenABER auf einem Kreis mit Radius 1 liegend (siehe Abb.).

(−1; 0).B.(1; 0).

(0; − 1). G.(0; 1).ABER.BEI.

Ebene Parallelität. Sind zwei Schnittgeraden einer Ebene jeweils parallel zu zwei Schnittgeraden einer anderen Ebene, so sind diese Ebenen parallel.
Nachweisen. Lassen a und b- Flugzeugdaten, eine 1 und eine 2- gerade Linien in der Ebene a, Schnittpunkt A, b 1 und b 2 die Linien parallel zu ihnen in der Ebene b. Nehmen wir an, die Flugzeuge a und b nicht parallel, das heißt, sie schneiden sich entlang einer Linie Mit. Gerade a 1 parallel zur Linie b 1, also parallel zur Ebene selbst b(ein Zeichen der Parallelität einer geraden Linie und einer Ebene). Gerade a 2 parallel zur Linie b2, es ist also parallel zur Ebene selbst. b(ein Zeichen der Parallelität einer geraden Linie und einer Ebene). Gerade Mit gehört zum Flugzeug a, also zumindest eine der Zeilen eine 1 oder eine 2überquert die Linie Mit, das heißt, es hat einen gemeinsamen Punkt damit. Aber gerade Mit gehört auch zum Flugzeug b, was bedeutet, dass die Linie überschritten wird Mit, gerade eine 1 oder eine 2 durchquert das Flugzeug b, was nicht sein kann, da die direkte eine 1 und eine 2 parallel zur Ebene b. Daraus folgt, dass die Flugzeuge a und b schneiden sich nicht, das heißt, sie sind parallel.

Satz 1 . Wenn sich zwei parallele Ebenen mit einer dritten schneiden, dann sind die Schnittlinien parallel.
Nachweisen. Lassen a und b sind parallele Ebenen, und g - die Ebene, die sie schneidet. Ebene a mit der Ebene schneiden g in einer geraden Linie a. Ebene b mit der Ebene schneiden g in einer geraden Linie b. Schnittlinien a und b in der gleichen Ebene liegen g und können daher entweder sich schneidende oder parallele Linien sein. Aber da sie zu zwei parallelen Ebenen gehören, können sie keine gemeinsamen Punkte haben. Daher sind sie parallel.

Satz 2. Segmente paralleler Linien, die zwischen zwei parallelen Ebenen eingeschlossen sind, sind gleich.
Nachweisen. Lassen a und b sind parallele Ebenen, und a und b sind parallele Linien, die sie schneiden. Durch gerade Linien a und b wir werden ausgeben Flugzeug g (Diese Linien sind parallel, also definieren Sie eine Ebene, und nur eine). Ebene a mit der Ebene schneiden g Gerade AB . Ebene b mit der Ebene schneiden g entlang der Linie SD. Nach dem vorherigen Satz ist die Linie Mit parallel zu einer Geraden d. Direkte a,b, AB und SD gehören zum Flugzeug g.Das von diesen Linien begrenzte Viereck ist ein Parallelogramm (seine gegenüberliegenden Seiten sind parallel). Und da es sich um ein Parallelogramm handelt, sind seine gegenüberliegenden Seiten gleich, dh AD \u003d BC

Die Parallelität von Ebenen ist ein Konzept, das erstmals vor mehr als zweitausend Jahren in der euklidischen Geometrie auftauchte.

Die Geburt dieser wissenschaftlichen Disziplin ist mit dem berühmten Werk des antiken griechischen Denkers Euklid verbunden, der im dritten Jahrhundert v. Chr. Die Broschüre „Anfänge“ verfasste. Unterteilt in dreizehn Bücher, waren die Elemente die höchste Errungenschaft der gesamten antiken Mathematik und stellten die grundlegenden Postulate dar, die mit den Eigenschaften ebener Figuren verbunden sind.

Die klassische Parallelitätsbedingung für Ebenen wurde wie folgt formuliert: Zwei Ebenen können als parallel bezeichnet werden, wenn sie keine gemeinsamen Punkte miteinander haben. Dies war das fünfte Postulat der euklidischen Arbeit.

Eigenschaften paralleler Ebenen

In der euklidischen Geometrie gibt es in der Regel fünf davon:

• Habe eins(beschreibt die Parallelität von Ebenen und ihre Einzigartigkeit). Durch einen Punkt, der außerhalb einer bestimmten gegebenen Ebene liegt, können wir genau eine Ebene parallel zu ihr ziehen

• Eigenschaft drei(mit anderen Worten, es wird die Eigenschaft einer geraden Linie genannt, die die Parallelität von Ebenen schneidet). Wenn eine einzelne gerade Linie eine dieser parallelen Ebenen schneidet, dann schneidet sie auch die andere.

• Eigenschaft vier(Eigenschaft von geraden Linien, die auf zueinander parallelen Ebenen geschnitten werden). Wenn sich zwei parallele Ebenen mit einer dritten (unter beliebigem Winkel) schneiden, sind auch die Schnittlinien parallel

• Eigenschaft fünften(eine Eigenschaft, die Segmente verschiedener paralleler Linien beschreibt, die zwischen zueinander parallelen Ebenen eingeschlossen sind). Die Segmente dieser parallelen Linien, die zwischen zwei parallelen Ebenen eingeschlossen sind, sind notwendigerweise gleich.

Parallelität von Ebenen in nichteuklidischen Geometrien

Solche Ansätze sind insbesondere die Geometrie von Lobachevsky und Riemann. Wenn Euklids Geometrie auf ebenen Flächen verwirklicht wurde, dann verwirklichte sich Lobatschewskis Geometrie in negativ gekrümmten Räumen (einfach gekrümmten), und bei Riemann findet sie ihre Verwirklichung in positiv gekrümmten Räumen (mit anderen Worten Kugeln). Es gibt eine sehr weit verbreitete stereotype Meinung, dass sich in Lobachevsky parallele Ebenen (und auch Linien) schneiden.

Dies ist jedoch nicht wahr. Tatsächlich war die Geburt der hyperbolischen Geometrie mit dem Beweis des fünften Postulats von Euklid und der Änderung der Ansichten darüber verbunden, aber die Definition paralleler Ebenen und Linien impliziert, dass sie sich weder in Lobachevsky noch in Riemann schneiden können, egal in welche Räume sie realisiert werden. Und die Änderung in Ansichten und Formulierungen war wie folgt. Das Postulat, dass durch einen Punkt, der nicht auf einer bestimmten Ebene liegt, nur eine parallele Ebene gezogen werden kann, wurde durch eine andere Formulierung ersetzt: durch einen Punkt, der nicht auf einer bestimmten bestimmten Ebene liegt, mindestens zwei Linien, die darin liegen dieselbe Ebene wie die gegebene und schneiden sie nicht.

Zwei Ebenen im Raum können parallel sein oder sich schneiden, wie in der folgenden Tabelle gezeigt.

Zeichen der Parallelität zweier Ebenen

Das erste Zeichen der Parallelität zweier Ebenen. Wenn zwei SchnittlinienSchnittlinien, jeweils in der gleichen Ebene liegend sind parallelsind parallel zwei Geraden, die in einer anderen Ebene liegen, dann sind solche Ebenen parallel.

Nachweisen . Betrachten Sie Abbildung 1, die die Ebenen α und β zeigt

Die Geraden a und b liegen in der Ebene α und schneiden sich im Punkt K . Die Linien c und d liegen in der Ebene β und sind parallel zu den Linien a bzw. b.

Wir werden das erste Zeichen der Parallelität zweier Ebenen mit der Methode des "Widerspruchs" beweisen. Dazu nehmen wir an, dass die Ebenen α und β nicht parallel sind. Daher müssen sich die Ebenen α und β schneiden, und zwar entlang einer geraden Linie. Wir bezeichnen die Gerade, entlang der sich die Ebenen α und β schneiden, mit dem Buchstaben l (Abb. 2) und verwenden das Zeichen der Parallelität der Geraden und der Ebene.

Die Ebene α verläuft parallel zur Linie c durch die Linie a und schneidet die Ebene β entlang der Linie l. Daher schließen wir aufgrund von , dass die Geraden a und l parallel sind. Gleichzeitig geht die Ebene α durch die Linie b parallel zur Linie d und schneidet die Ebene β entlang der Linie l. Von hier aus schließen wir aufgrund des Attributs der Parallelität der Linie und der Ebene, dass die Linien b und l parallel sind. Somit haben wir erhalten, dass zwei Geraden durch den Punkt K auf der Ebene α verlaufen, nämlich die Geraden a und b , die parallel zur Linie l sind. Der daraus resultierende Widerspruch mit Axiom paralleler Geraden lässt sich behaupten, dass die Annahme, dass sich die Ebenen α und β schneiden, falsch ist. Der Beweis des ersten Kriteriums für die Parallelität zweier Ebenen ist abgeschlossen.

Das zweite Zeichen der Parallelität zweier Ebenen. Wenn zwei sich schneidende Geraden, die in einer Ebene liegen, parallel zu einer anderen Ebene sind, dann sind solche Ebenen parallel.

Nachweisen . Betrachten Sie Abbildung 3, die die Ebenen α und β zeigt.

Diese Figur zeigt auch die Linien a und b, die in der Ebene α liegen und sich im Punkt K schneiden. Nach Annahme ist jede der Linien a und b parallel zur Ebene β. Es ist zu beweisen, dass die Ebenen α und β parallel sind.

Der Beweis dieser Behauptung ist analog zum Beweis des ersten Kriteriums für die Parallelität zweier Ebenen, und wir überlassen ihn dem Leser als nützliche Übung.

Auf unserer Website können Sie sich auch mit den Unterrichtsmaterialien vertraut machen, die von den Lehrern des Resolventa-Schulungszentrums zur Vorbereitung auf die Prüfung in Mathematik entwickelt wurden.