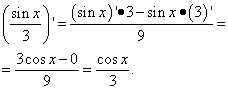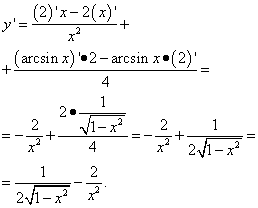Bei der Ableitung der allerersten Formel der Tabelle gehen wir von der Definition der Ableitung einer Funktion an einem Punkt aus. Nehmen wir wo x- jede reelle Zahl, das heißt, x– beliebige Nummer aus dem Funktionsdefinitionsbereich . Schreiben wir die Grenze des Verhältnisses des Funktionsinkrements zum Argumentinkrement zu: ![]()
Es ist zu beachten, dass unter dem Vorzeichen des Grenzwerts ein Ausdruck erhalten wird, der nicht die Unsicherheit von Null geteilt durch Null ist, da der Zähler keinen infinitesimalen Wert enthält, sondern genau Null. Mit anderen Worten, das Inkrement einer konstanten Funktion ist immer Null.
Auf diese Weise, Ableitung einer konstanten Funktionauf dem gesamten Definitionsbereich gleich Null ist.
Ableitung einer Potenzfunktion.
Die Formel für die Ableitung einer Potenzfunktion hat die Form ![]() , wobei der Exponent p ist eine beliebige reelle Zahl.
, wobei der Exponent p ist eine beliebige reelle Zahl.
Beweisen wir zunächst die Formel für den natürlichen Exponenten, also z p = 1, 2, 3, ...
Wir verwenden die Definition eines Derivats. Schreiben wir die Grenze des Verhältnisses des Inkrements der Potenzfunktion zum Inkrement des Arguments: 
Um den Ausdruck im Zähler zu vereinfachen, wenden wir uns der Binomialformel von Newton zu: 
Folglich, 
Damit ist die Formel für die Ableitung einer Potenzfunktion für einen natürlichen Exponenten bewiesen.
Ableitung der Exponentialfunktion.
Wir leiten die Ableitungsformel basierend auf der Definition ab:
Kam in die Ungewissheit. Um es zu erweitern, führen wir eine neue Variable ein, und für . Dann . Beim letzten Übergang haben wir die Formel für den Übergang zu einer neuen Basis des Logarithmus verwendet.
Führen wir eine Substitution in der ursprünglichen Grenze durch: 
Erinnern wir uns an die zweite bemerkenswerte Grenze, dann kommen wir zur Formel für die Ableitung der Exponentialfunktion: 
Ableitung einer logarithmischen Funktion.
Beweisen wir die Formel für die Ableitung der logarithmischen Funktion für alle x aus dem Geltungsbereich und alle gültigen Basiswerte a Logarithmus. Per Definition der Ableitung haben wir: 
Wie Sie bemerkt haben, wurden die Transformationen im Beweis unter Verwendung der Eigenschaften des Logarithmus durchgeführt. Gleichberechtigung  gilt wegen der zweiten bemerkenswerten Grenze.
gilt wegen der zweiten bemerkenswerten Grenze.
Ableitungen trigonometrischer Funktionen.
Um Formeln für Ableitungen trigonometrischer Funktionen herzuleiten, müssen wir uns einige trigonometrische Formeln sowie den ersten bemerkenswerten Grenzwert ins Gedächtnis rufen.
Per Definition der Ableitung für die Sinusfunktion haben wir ![]() .
.
Wir verwenden die Formel für die Sinusdifferenz: 
Bleibt noch die erste bemerkenswerte Grenze: 
Also die Ableitung der Funktion Sünde x Es gibt cos x.
Die Formel für die Kosinusableitung beweist man genauso. 
Also die Ableitung der Funktion cos x Es gibt – Sünde x.
Die Ableitung von Formeln für die Ableitungstabelle für Tangens und Kotangens erfolgt nach den bewährten Ableitungsregeln (Ableitung eines Bruchs). 
Ableitungen hyperbolischer Funktionen.
Die Ableitungsregeln und die Ableitungsformel der Exponentialfunktion aus der Ableitungstabelle erlauben es uns, Formeln für die Ableitungen des hyperbolischen Sinus, Cosinus, Tangens und Kotangens herzuleiten. 
Ableitung der Umkehrfunktion.
Damit es bei der Darstellung keine Verwirrung gibt, bezeichnen wir im unteren Index das Argument der Funktion, mit dem die Differenzierung durchgeführt wird, dh es ist die Ableitung der Funktion f(x) an x.
Jetzt formulieren wir Regel zum Finden der Ableitung der Umkehrfunktion.
Lassen Sie die Funktionen y = f(x) und x = g(y) gegenseitig invers, definiert auf den Intervallen bzw. Wenn an einem Punkt eine endliche Nicht-Null-Ableitung der Funktion existiert f(x), dann existiert an dem Punkt eine endliche Ableitung der Umkehrfunktion g(y), und ![]() . In einem anderen Eintrag
. In einem anderen Eintrag ![]() .
.
Diese Regel kann beliebig umformuliert werden x aus dem Intervall , dann bekommen wir  .
.
Lassen Sie uns die Gültigkeit dieser Formeln überprüfen.
Finden wir die Umkehrfunktion für den natürlichen Logarithmus ![]() (hier j ist eine Funktion, und x- Streit). Lösen Sie diese Gleichung für x, wir bekommen (hier x ist eine Funktion, und j ihr Argument). Also,
(hier j ist eine Funktion, und x- Streit). Lösen Sie diese Gleichung für x, wir bekommen (hier x ist eine Funktion, und j ihr Argument). Also, ![]() und zueinander inverse Funktionen.
und zueinander inverse Funktionen.
Aus der Tabelle der Derivate sehen wir das ![]() und
und ![]() .
.
Stellen wir sicher, dass die Formeln zum Finden von Ableitungen der Umkehrfunktion uns zu den gleichen Ergebnissen führen: 
Thema:"Derivat trigonometrische Funktionen».
Unterrichtsart- Lektion zur Festigung des Wissens.
Unterrichtsformular- ein integrierter Unterricht.
Der Platz des Unterrichts im Unterrichtssystem für diesen Abschnitt- allgemeiner Unterricht.
Ziele werden umfassend festgelegt:
- lehrreich: die Ableitungsregeln kennen, die Ableitungsregeln beim Lösen von Gleichungen und Ungleichungen anwenden können; verbessern Fach, einschließlich Computer, Fähigkeiten und Fertigkeiten; Computerfähigkeiten;
- Entwicklung: Entwicklung intellektueller und logischer Fähigkeiten und kognitiver Interessen;
- lehrreich: Anpassungsfähigkeit entwickeln modernen Bedingungen Lernen.
Methoden:
- reproduktiv und produktiv;
- praktisch und verbal;
- unabhängige Arbeit;
- programmiertes Lernen, T.S.O.;
- eine Kombination aus Frontal-, Gruppen- und Einzelarbeit;
- differenziertes Lernen;
- induktiv deduktiv.
Formen der Kontrolle:
- mündliche Befragung,
- programmierte Steuerung,
- selbstständige Arbeit,
- individuelle Aufgaben am Computer,
- gegenseitige Kontrolle anhand des Schüler-Diagnoseausweises.
WÄHREND DER KLASSEN
I. Organisatorischer Moment
II. Aktualisierung des Grundwissens
a) Zielkommunikation:
- die Ableitungsregeln kennen, die Ableitungsregeln beim Lösen von Problemen, Gleichungen und Ungleichungen anwenden können;
- verbessern Fach, einschließlich Computer, Fähigkeiten und Fertigkeiten; Computerfähigkeiten;
- intellektuelle und logische Fähigkeiten und kognitive Interessen entwickeln;
- Anpassungsfähigkeit an moderne Lernbedingungen erziehen.
b) Wiederholung von Lehrmaterial
Regeln zur Berechnung von Ableitungen (Wiederholung von Formeln auf einem Computer mit Ton). doc.7.
- Was ist die Ableitung des Sinus?
- Was ist die Ableitung des Kosinus?
- Was ist die Ableitung der Tangente?
- Was ist die Ableitung des Kotangens?
III. Mündliche Arbeit
Derivat finden. |
|||
Variante 1. |
Option 2. |
||
bei = 2X + 5. |
bei = 2X – 5. |
||
bei= 4 cos X. |
bei= 3 Sünde X. |
||
bei=tg X+ctg X. |
bei=tg X– ctg X. |
||
bei= Sünde 3 X. |
bei= cos4 X. |
||
Antwortmöglichkeiten. |
|||
– 4 Sünde X |
– 3 cos X |
||
1/cos 2 X+ 1/sünde 2 X |
1/cos 2 X–1/sin2 X |
1/sünde2 X–1/cos 2 X |
|
– 4sin4 X |
– 3cos3 X |
||
Hefte tauschen. Markieren Sie in den Diagnosekarten richtig erledigte Aufgaben mit einem + Zeichen und falsch erledigte Aufgaben mit einem - Zeichen.
IV. Lösen von Gleichungen mit der Ableitung
– Wie finde ich die Punkte, an denen die Ableitung gleich Null ist?
Um die Punkte zu finden, an denen die Ableitung einer bestimmten Funktion gleich Null ist, benötigen Sie:
- Bestimmung der Art der Funktion,
- Bereich finden Funktionsdefinitionen,
- Finden Sie die Ableitung dieser Funktion,
- löse die Gleichung f "(x) = 0,
- Wähle die richtige Antwort.
Aufgabe 1.
Gegeben: bei
= X– Sünde x.
Finden: Punkte, an denen die Ableitung Null ist.
Lösung. Die Funktion ist auf der Menge aller reellen Zahlen definiert und differenzierbar, da die Funktionen auf der Menge aller reellen Zahlen definiert und differenzierbar sind g(x) = x und t(x) = –sünde x.
Mit den Ableitungsregeln erhalten wir f
"(x) = (x– Sünde x)" = (x)" – (Sünde x)" = 1 – cos x.
Wenn ein f "(x) = 0, dann 1 – cos x = 0.
cos x= 1/; Wenn wir die Irrationalität im Nenner loswerden, erhalten wir cos x
= /2.
Nach der Formel t= ± arccos a+ 2n, n Z erhalten wir: X= ± arccos /2 + 2n, nZ.
Antworten: x = ± /4 + 2n, nZ.
V. Lösen von Gleichungen mit einem Algorithmus
Finden Sie heraus, an welchen Stellen die Ableitung verschwindet.
f(x) = Sünde x+ cos x |
f(x) = Sünde2 x – x |
f(x) = 2x+ cos(4 x – ) |
Der Schüler kann eines der drei Beispiele auswählen. Das erste Beispiel wird anhand der Punktzahl " 3 ", zweite - " 4 ", dritte - " 5 ". Lösung in Notebooks mit anschließender gegenseitiger Verifikation. Ein Schüler entscheidet an der Tafel. Wenn sich herausstellt, dass die Lösung falsch ist, muss der Schüler zum Algorithmus zurückkehren und versuchen, ihn erneut zu lösen.
Programmierte Steuerung.
Variante 1 |
Option 2 |
|||
j = 2X 3 |
j = 3X 2 |
|||
j = 1/4 X 4 + 2X 2 – 7 |
j = 1/2 X 4 + 4X + 5 |
|||
j = X 3 + 4X 2
– 3X. |
j = 2X 3 – 9X 2
+ 12X + 7. |
|||
j= Sünde 2 X– cos 3 X. |
j= cos2 X– Sünde 3 X. |
|||
j=tg X-ctg( X + /4). |
j=ctg X+tg( X – /4). |
|||
j= Sünde 2 X. |
j= cos2 X. |
|||
Antwortmöglichkeiten. |
||||
|
Die Ableitungen inverser trigonometrischer Funktionen und die Ableitung ihrer Formeln werden vorgestellt. Ausdrücke von Ableitungen höherer Ordnung sind ebenfalls angegeben. Links zu Seiten mit einer ausführlicheren Darstellung der Herleitung von Formeln. Zuerst leiten wir die Formel für die Ableitung des Arkussinus her. Lassen Weil dann . Dann Genau so erhält man die Formel für die Ableitung des Arkuskosinus. Es ist jedoch einfacher, die Formel zu verwenden, die inverse trigonometrische Funktionen verbindet: Eine ausführlichere Darstellung findet sich auf der Seite „Herleitung von Ableitungen des Arkussinus und Arkuskosinus“. Es ist gegeben Ableitung von Derivaten auf zwei Arten- oben betrachtet und nach der Formel der Ableitung der Umkehrfunktion. Ableitung von Ableitungen von Arkustangens und ArkotangensAuf die gleiche Weise finden wir die Ableitungen von Arkustangens und Arkotangens. Lassen Ableitung des inversen Tangens: Arcussinus-DerivateLassen Durch Differenzieren dieser Gleichung kann man Ableitungen höherer Ordnung finden. Ableitung des Arkussinus n-ter OrdnungDie Ableitung des Arkussinus n-ter Ordnung hat nächste Ansicht: Das Polynom erfüllt die Differentialgleichung: Ableitung des Arkuskosinus n-ter OrdnungDie Ableitungen für den Arkuskosinus erhält man aus den Ableitungen für den Arkussinus mit der trigonometrischen Formel: Arcustangens-AbleitungenLassen . Wir haben die Ableitung erster Ordnung des inversen Tangens gefunden: Zerlegen wir den Bruch in einfache: Zeiten differenzieren und den Bruch auf einen gemeinsamen Nenner bringen: Einsetzend erhalten wir: Ableitung des Arkustangens n-ter OrdnungSomit kann die Ableitung des Arkustangens n-ter Ordnung auf verschiedene Arten dargestellt werden: Ableitungen des inversen TangensLassen Sie jetzt. Wenden wir die Formel an, die die inversen trigonometrischen Funktionen verbindet: Einsetzend finden wir: Verweise: Aus dem Studium der Geometrie und Mathematik sind Schüler daran gewöhnt, dass ihnen der Begriff einer Ableitung durch den Bereich der Figur, Differentiale, Funktionsgrenzen und auch Grenzen vermittelt wird. Lassen Sie uns versuchen, das Konzept einer Ableitung aus einem anderen Blickwinkel zu betrachten und festzustellen, wie die Ableitungs- und trigonometrischen Funktionen verknüpft werden können. Stellen Sie sich also eine beliebige Kurve vor, die durch eine abstrakte Funktion y = f(x) beschrieben wird. Stellen Sie sich vor, dass der Graph eine Karte einer Touristenroute ist. Das Inkrement ∆x (Delta x) in der Abbildung ist eine bestimmte Entfernung des Weges, und ∆y ist die Änderung der Höhe des Weges über dem Meeresspiegel. Wenn der Veranstalter der Wanderung die Werte für den Start- und Endpunkt des Wanderweges, also ∆x – einnimmt, werden diese sein gleich lang Route, kann es keine objektiven Daten über den Schwierigkeitsgrad der Reise erhalten. Daher ist es notwendig, einen weiteren Graphen zu erstellen, der die Geschwindigkeit und „Qualität“ von Pfadänderungen charakterisiert, dh das Verhältnis ∆x/∆y für jeden „Meter“ der Route bestimmt. Dieses Diagramm ist eine visuelle Ableitung für einen bestimmten Pfad und beschreibt objektiv seine Änderungen in jedem interessierenden Intervall. Es ist sehr einfach, dies zu überprüfen, der Wert von ∆x/∆y ist nichts anderes als das Differential, das für einen bestimmten Wert von x und y genommen wird. Differenzieren wir nicht auf bestimmte Koordinaten, sondern auf die Funktion als Ganzes:
Ableitungs- und trigonometrische FunktionenTrigonometrische Funktionen sind untrennbar mit der Ableitung verbunden. Sie können dies anhand der folgenden Zeichnung verstehen. Die Abbildung der Koordinatenachse zeigt die Funktion Y = f (x) - die blaue Kurve. K (x0; f (x0)) ist ein beliebiger Punkt, x0 + ∆x ist ein Inkrement entlang der OX-Achse und f (x0 + ∆x) ist ein Inkrement entlang der OY-Achse an einem Punkt L.
Ziehe eine Linie durch die Punkte K und L und konstruiere rechtwinkliges Dreieck KLN. Wenn Sie das Segment LN gedanklich entlang des Diagramms Y = f (x) verschieben, tendieren die Punkte L und N zu den Werten K (x0; f (x0)). Nennen wir diesen Punkt den bedingten Anfang des Graphen - die Grenze, aber wenn die Funktion unendlich ist, zumindest in einem der Intervalle - wird dieses Streben auch unendlich sein und sein Grenzwert liegt nahe bei 0. Die Natur dieses Strebens kann durch eine Tangente an den ausgewählten Punkt y = kx + b oder durch den Graphen der Ableitung der ursprünglichen Funktion dy - die grüne Gerade - beschrieben werden. Aber wo ist hier die Trigonometrie?! Es ist sehr einfach, ein rechtwinkliges Dreieck KLN zu betrachten. Der Wert des Differentials für einen bestimmten Punkt K ist der Tangens des Winkels α oder ∠K:
Somit ist es möglich, die geometrische Bedeutung der Ableitung und ihre Beziehung zu trigonometrischen Funktionen zu beschreiben. Ableitungsformeln für trigonometrische FunktionenDie Transformationen von Sinus, Kosinus, Tangens und Kotangens zur Bestimmung der Ableitung müssen auswendig gelernt werden.
Die letzten beiden Formeln sind kein Fehler, Tatsache ist, dass es einen Unterschied zwischen der Definition der Ableitung eines einfachen Arguments und einer Funktion in derselben Eigenschaft gibt. In Betracht ziehen Vergleichstabelle mit Formeln für Ableitungen von Sinis, Kosinus, Tangens und Kotangens:
Formeln für die Ableitungen von Arkussinus, Arkuskosinus, Arkustangens und Arkuskotangens werden ebenfalls abgeleitet, obwohl sie äußerst selten verwendet werden:
Es sei darauf hingewiesen, dass die obigen Formeln eindeutig nicht ausreichen erfolgreiche Lösung typische USE-Aufgaben, die beim Lösen demonstriert werden Fallstudie Suche nach der Ableitung eines trigonometrischen Ausdrucks. Übung: Es ist notwendig, die Ableitung der Funktion und ihren Wert für π/4 zu finden:
Lösung: Um y’ zu finden, müssen Sie sich an die grundlegenden Formeln für die Umwandlung der ursprünglichen Funktion in eine Ableitung erinnern, nämlich. Zur Findung Ableitung einer trigonometrischen Funktion verwenden müssen Ableitungstabelle, nämlich Derivate 6-13. Wenn gefunden Ableitungen einfacher trigonometrischer Funktionen Um häufige Fehler zu vermeiden, beachten Sie die folgenden Punkte:
Beispiel 1 Finden Sie die Ableitung einer Funktion Lösung. Sagen wir mit Kosinus-Ableitung Alles ist klar, werden viele sagen, die anfangen, Derivate zu studieren. Wie wäre es mit Sinus-Ableitung Zwölf geteilt durch Pi? Antwort: Betrachten Sie gleich Null! Hier ist der Sinus (immerhin eine Funktion!) eine Falle, weil das Argument nicht die Variable x oder irgendeine andere Variable ist, sondern nur eine Zahl. Das heißt, der Sinus dieser Zahl ist auch eine Zahl. Und die Ableitung einer Zahl (Konstante), wie wir aus der Ableitungstabelle wissen, ist gleich Null. Also lassen wir nur den Minus-Sinus von x und finden seine Ableitung, ohne das Vorzeichen zu vergessen:
Beispiel 2 Finden Sie die Ableitung einer Funktion
Lösung. Der zweite Term ist derselbe Fall wie der erste Term im vorherigen Beispiel. Das heißt, eine Zahl, und die Ableitung der Zahl ist Null. Die Ableitung des zweiten Terms finden wir als Ableitung des Quotienten:
Beispiel 3 Finden Sie die Ableitung einer Funktion Lösung. Das ist eine andere Aufgabe: Hier im ersten Term gibt es weder einen Arkussinus noch eine andere trigonometrische Funktion, aber es gibt x, was bedeutet, dass dies eine Funktion von x ist. Daher differenzieren wir es als Term in der Summe der Funktionen:
Hier waren Geschicklichkeit bei Aktionen mit Fraktionen gefragt, nämlich bei der Eliminierung der dreistöckigen Fraktion. Beispiel 4 Finden Sie die Ableitung einer Funktion
Lösung. Hier spielt der Buchstabe "fi" die gleiche Rolle wie "X" in den vorherigen Fällen (und in den meisten anderen, aber nicht in allen) - eine unabhängige Variable. Wenn wir also nach der Ableitung des Produkts von Funktionen suchen, werden wir uns nicht beeilen, die Ableitung der Wurzel von „phi“ gleich Null zu erklären. So:
Aber die Lösung endet nicht dort. Da ähnliche Glieder in zwei Klammern zusammengefasst werden, müssen wir den Ausdruck noch umformen (vereinfachen). Deshalb multiplizieren wir die Klammern mit den daraus entfernten Faktoren, bringen die Terme dann auf einen gemeinsamen Nenner und führen weitere elementare Transformationen durch:
Beispiel 5 Finden Sie die Ableitung einer Funktion Lösung. In diesem Beispiel müssen wir die Tatsache kennen, dass es eine solche trigonometrische Funktion – Sekans – und ihre Formeln in Bezug auf den Kosinus gibt. Unterscheiden:
Beispiel 6 Finden Sie die Ableitung einer Funktion
Lösung. In diesem Beispiel müssen wir uns die Doppelwinkelformel aus dem Schulkurs merken. Aber zuerst differenzieren wir:
(Dies ist die Doppelwinkelformel) Der Artikel hat Ihnen gefallen? Mit Freunden teilen!
Teilen Sie weiter Facebook
Lesen Sie auch
oben
| ||||