Parallele Linien. Visueller Leitfaden (2019)

Das Konzept der parallelen Linien

Bestimmung 1

Parallele Linien- Linien, die in derselben Ebene liegen, fallen nicht zusammen und haben keine gemeinsamen Punkte.

Wenn Linien einen gemeinsamen Punkt haben, dann sie schneiden.

Wenn alle Punkte der Linien passen, dann haben wir im Wesentlichen eine Gerade.

Liegen die Geraden in unterschiedlichen Ebenen, so gelten etwas mehr Bedingungen für ihre Parallelität.

Wenn wir gerade Linien auf derselben Ebene betrachten, können wir die folgende Definition geben:

Bestimmung 2

Zwei Linien in einer Ebene werden aufgerufen parallel wenn sie sich nicht schneiden.

In der Mathematik werden parallele Geraden üblicherweise mit dem Parallelzeichen „$\parallel$“ gekennzeichnet. Beispielsweise wird die Tatsache, dass die Linie $c$ parallel zur Linie $d$ verläuft, wie folgt bezeichnet:

$c \parallel d$.

Das Konzept paralleler Segmente wird oft in Betracht gezogen.

Bestimmung 3

Die beiden Segmente werden aufgerufen parallel wenn sie auf parallelen Linien liegen.

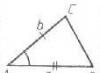
In der Abbildung sind beispielsweise die Segmente $AB$ und $CD$ parallel, weil sie gehören zu parallelen Linien:

$AB\parallele CD$.

Allerdings sind die Segmente $MN$ und $AB$ bzw. $MN$ und $CD$ nicht parallel. Diese Tatsache kann mit Symbolen wie folgt geschrieben werden:

$MN ∦ AB$ und $MN ∦ CD$.

Die Parallelität einer Geraden und eines Segments, einer Geraden und eines Strahls, eines Segments und eines Strahls oder zweier Strahlen wird auf ähnliche Weise bestimmt.

Geschichtlicher Bezug

AUS griechisch Der Begriff "parallelos" wird mit "nebeneinander gehen" oder "nebeneinander ausgeführt" übersetzt. Der Begriff wurde in der alten Schule von Pythagoras verwendet, bevor parallele Linien definiert wurden. Entsprechend historische Fakten Euklid im $III$ c. BC. In seinen Schriften wurde jedoch die Bedeutung des Begriffs der parallelen Linien offenbart.

In der Antike hatte das Zeichen für parallele Linien eine andere Form als das, was wir in der modernen Mathematik verwenden. Zum Beispiel der altgriechische Mathematiker Pappus im $III$ c. ANZEIGE Parallelität wurde durch ein Gleichheitszeichen gekennzeichnet. Diese. die Tatsache, dass die Linie $l$ parallel zur Linie $m$ verläuft, wurde früher mit "$l=m$" bezeichnet. Später begannen sie, das bekannte Zeichen „$\parallel$“ zu verwenden, um die Parallelität von geraden Linien anzuzeigen, und das Gleichheitszeichen wurde verwendet, um die Gleichheit von Zahlen und Ausdrücken anzuzeigen.

Parallele Linien im Leben

Oft bemerken wir nicht, dass wir im normalen Leben von einer Vielzahl paralleler Linien umgeben sind. Beispielsweise wird in einem Musikbuch und einer Sammlung von Liedern mit Noten das Notensystem mit parallelen Linien erstellt. Ebenfalls parallele Linien finden sich auch in Musikinstrumenten (z. B. Harfensaiten, Gitarren, Klaviertasten usw.).

Parallel verlaufen auch elektrische Leitungen, die entlang der Straßen und Straßen verlaufen. Metrolinien u Eisenbahnen sind parallel angeordnet.

Parallelen finden sich neben dem Alltag in der Malerei, in der Architektur, im Bau von Gebäuden.

Parallele Linien in der Architektur

In den präsentierten Bildern enthalten architektonische Strukturen parallele Linien. Die Verwendung paralleler Linien in der Konstruktion trägt dazu bei, die Lebensdauer solcher Strukturen zu verlängern und verleiht ihnen außergewöhnliche Schönheit, Attraktivität und Erhabenheit. Auch Stromleitungen werden bewusst parallel geführt, um Kreuzungen oder Berührungen zu vermeiden, die zu Kurzschlüssen, Unterbrechungen und Stromausfällen führen würden. Damit sich der Zug frei bewegen kann, sind die Schienen auch in parallelen Linien ausgeführt.

In der Malerei werden parallele Linien als zu einer Linie zusammenlaufend oder nahe daran dargestellt. Diese Technik wird Perspektive genannt, die aus der Illusion des Sehens folgt. Wenn Sie lange in die Ferne schauen, sehen parallele Linien wie zwei konvergierende Linien aus.

In diesem Artikel geht es um parallele Linien und um parallele Linien. Zuerst wird die Definition von parallelen Linien in der Ebene und im Raum gegeben, die Notation eingeführt, Beispiele und grafische Darstellungen von parallelen Linien gegeben. Außerdem werden die Zeichen und Bedingungen der Parallelität von geraden Linien analysiert. Abschließend werden Lösungen für typische Probleme des Parallelitätsnachweises von Geraden gezeigt, die durch einige Geradengleichungen in einem rechtwinkligen Koordinatensystem in einer Ebene und im dreidimensionalen Raum gegeben sind.

Seitennavigation.

Parallele Linien - grundlegende Informationen.

Definition.

Zwei Linien in einer Ebene werden aufgerufen parallel wenn sie keine gemeinsamen Punkte haben.

Definition.

Zwei Linien in drei Dimensionen werden genannt parallel wenn sie in der gleichen Ebene liegen und keine gemeinsamen Punkte haben.

Beachten Sie, dass die Klausel "wenn sie in derselben Ebene liegen" in der Definition paralleler Linien im Raum sehr wichtig ist. Lassen Sie uns diesen Punkt klarstellen: Zwei gerade Linien im dreidimensionalen Raum, die keine gemeinsamen Punkte haben und nicht in derselben Ebene liegen, sind nicht parallel, sondern schief.

Hier sind einige Beispiele für parallele Linien. Die gegenüberliegenden Ränder des Notizbuchblattes liegen auf parallelen Linien. Die geraden Linien, entlang denen die Ebene der Hauswand die Ebenen der Decke und des Bodens schneidet, sind parallel. Bahngleise in der Ebene können auch als parallele Linien betrachtet werden.

Das Symbol "" wird verwendet, um parallele Linien zu bezeichnen. Das heißt, wenn die Linien a und b parallel sind, dann kannst du kurz ein b schreiben.

Beachten Sie, dass wenn die Linien a und b parallel sind, wir sagen können, dass Linie a parallel zu Linie b ist, und dass auch Linie b parallel zu Linie a ist.

Lassen Sie uns eine Aussage äußern, die beim Studium paralleler Linien in der Ebene eine wichtige Rolle spielt: Durch einen Punkt, der nicht auf einer gegebenen Linie liegt, verläuft die einzige Parallele zu der gegebenen. Diese Aussage wird als Tatsache akzeptiert (sie kann nicht auf der Grundlage der bekannten Axiome der Planimetrie bewiesen werden) und wird das Axiom der parallelen Linien genannt.

Für den Fall im Raum gilt der Satz: Durch jeden Punkt im Raum, der nicht auf einer gegebenen Geraden liegt, geht eine einzige Gerade parallel zu der gegebenen. Dieser Satz lässt sich leicht mit dem oben angegebenen Parallelenaxiom beweisen (den Beweis findet man im Geometrielehrbuch für die Klassen 10-11, das am Ende des Artikels im Literaturverzeichnis aufgeführt ist).

Für den Fall im Raum gilt der Satz: Durch jeden Punkt im Raum, der nicht auf einer gegebenen Geraden liegt, geht eine einzige Gerade parallel zu der gegebenen. Dieser Satz lässt sich leicht mit dem oben angegebenen Parallelenaxiom beweisen.

Parallelität von Linien - Zeichen und Bedingungen der Parallelität.

Ein Zeichen für parallele Linien ist eine hinreichende Bedingung für parallele Linien, also eine solche Bedingung, deren Erfüllung parallele Linien garantiert. Mit anderen Worten, die Erfüllung dieser Bedingung reicht aus, um die Tatsache auszusagen, dass die Linien parallel sind.

Es gibt auch notwendige und hinreichende Bedingungen für parallele Linien in der Ebene und im dreidimensionalen Raum.

Lassen Sie uns die Bedeutung des Ausdrucks "notwendige und hinreichende Bedingung für parallele Linien" erklären.

Die hinreichende Bedingung für parallele Linien haben wir bereits behandelt. Und was ist " notwendige Bedingung parallele Linien? Durch den Namen "notwendig" wird deutlich, dass die Erfüllung dieser Bedingung notwendig ist, damit die Linien parallel sind. Mit anderen Worten, wenn die notwendige Bedingung für parallele Linien nicht erfüllt ist, dann sind die Linien nicht parallel. Auf diese Weise, notwendige und hinreichende Bedingung für die Parallelität von Leitungen ist eine Bedingung, deren Erfüllung für Parallelleitungen sowohl notwendig als auch hinreichend ist. Das heißt, dies ist einerseits ein Zeichen für parallele Linien und andererseits eine Eigenschaft, die parallele Linien haben.

Bevor wir die notwendige und hinreichende Bedingung für die Parallelität von Linien angeben, ist es nützlich, einige Hilfsdefinitionen in Erinnerung zu rufen.

Sekantenlinie ist eine Gerade, die jede der beiden gegebenen nicht übereinstimmenden Geraden schneidet.

Am Schnittpunkt zweier Sekantenlinien werden acht nicht eingesetzte Linien gebildet. Die sogenannte querliegend, korrespondierend und einseitige Ecken. Lassen Sie uns sie auf der Zeichnung zeigen.

Satz.

Wenn zwei Geraden in einer Ebene von einer Sekante geschnitten werden, dann ist es für ihre Parallelität notwendig und ausreichend, dass die kreuzweise liegenden Winkel gleich oder sind entsprechende Winkel gleich waren oder die Summe einseitiger Winkel gleich 180 Grad war.

Lassen Sie uns diese notwendige und hinreichende Bedingung für parallele Linien in der Ebene grafisch veranschaulichen.

Beweise für diese Bedingungen für parallele Linien finden Sie in Geometrie-Lehrbüchern für die Klassen 7-9.

Beachten Sie, dass diese Bedingungen auch im dreidimensionalen Raum verwendet werden können - Hauptsache, die beiden Geraden und die Sekante liegen in derselben Ebene.

Hier sind ein paar weitere Sätze, die oft beim Beweis der Parallelität von Linien verwendet werden.

Satz.

Wenn zwei Geraden in einer Ebene parallel zu einer dritten Geraden sind, dann sind sie parallel. Der Beweis dieser Eigenschaft folgt aus dem Axiom der Parallelen.

Eine ähnliche Bedingung gilt für parallele Linien im dreidimensionalen Raum.

Satz.

Wenn zwei Linien im Raum parallel zu einer dritten Linie sind, dann sind sie parallel. Der Nachweis dieser Eigenschaft wird im Geometrieunterricht der 10. Klasse berücksichtigt.

Lassen Sie uns die stimmhaften Theoreme veranschaulichen.

Geben wir noch einen Satz an, mit dem wir die Parallelität von Linien in der Ebene beweisen können.

Satz.

Wenn zwei Geraden in einer Ebene senkrecht zu einer dritten Geraden stehen, dann sind sie parallel.

Es gibt einen ähnlichen Satz für Linien im Raum.

Satz.

Stehen zwei Linien im dreidimensionalen Raum senkrecht auf derselben Ebene, dann sind sie parallel.

Lassen Sie uns Bilder zeichnen, die diesen Sätzen entsprechen.

Alle oben formulierten Sätze, Vorzeichen und notwendigen und hinreichenden Bedingungen sind hervorragend geeignet, um die Parallelität von Geraden mit Methoden der Geometrie zu beweisen. Das heißt, um die Parallelität zweier gegebener Geraden zu beweisen, muss man zeigen, dass sie parallel zur dritten Geraden sind, oder die Gleichheit von sich kreuzenden Winkeln zeigen usw. Viele dieser Probleme werden im Geometrieunterricht gelöst weiterführende Schule. Es sollte jedoch beachtet werden, dass es in vielen Fällen bequem ist, die Koordinatenmethode zu verwenden, um die Parallelität von Linien in einer Ebene oder im dreidimensionalen Raum zu beweisen. Formulieren wir die notwendigen und hinreichenden Bedingungen für die Parallelität von Geraden, die in einem rechtwinkligen Koordinatensystem gegeben sind.

Parallelität von Linien in einem rechtwinkligen Koordinatensystem.

In diesem Abschnitt des Artikels werden wir formulieren notwendige und hinreichende Bedingungen für Parallelleitungen in einem rechtwinkligen Koordinatensystem, abhängig von der Art der Gleichungen, die diese Linien bestimmen, und wir werden auch detaillierte Lösungen für typische Probleme geben.

Beginnen wir mit der Bedingung der Parallelität zweier Geraden in der Ebene im rechtwinkligen Koordinatensystem Oxy . Sein Beweis basiert auf der Definition des Richtungsvektors der Linie und der Definition des Normalenvektors der Linie auf der Ebene.

Satz.

Damit zwei nicht zusammenfallende Geraden in einer Ebene parallel sind, ist es notwendig und ausreichend, dass die Richtungsvektoren dieser Geraden kollinear sind oder die Normalenvektoren dieser Geraden kollinear sind oder der Richtungsvektor einer Geraden senkrecht zur Normalen steht Vektor der zweiten Zeile.

Offensichtlich reduziert sich die Bedingung der Parallelität zweier Linien in der Ebene auf (Richtungsvektoren von Linien oder Normalenvektoren von Linien) oder auf (Richtungsvektor einer Linie und Normalenvektor der zweiten Linie). Also, wenn und sind die Richtungsvektoren der Linien a und b, und und die Normalenvektoren der Geraden a bzw. b sind, dann kann die notwendige und hinreichende Bedingung für parallele Geraden a und b geschrieben werden als , oder , oder , wobei t eine reelle Zahl ist. Aus den bekannten Geradengleichungen werden wiederum die Koordinaten der Richtungs- und (oder) Normalenvektoren der Geraden a und b ermittelt.

Insbesondere wenn die Linie a im rechtwinkligen Koordinatensystem Oxy auf der Ebene definiert, definiert die allgemeine Liniengleichung die Form , und die Gerade b - , dann haben die Normalenvektoren dieser Linien die Koordinaten bzw. und die Bedingung der Parallelität der Linien a und b wird geschrieben als .

Entspricht die Gerade a der Gleichung der Geraden mit dem Steigungsbeiwert der Form . Wenn also Linien in einer Ebene in einem rechtwinkligen Koordinatensystem parallel sind und durch Liniengleichungen mit Steigungskoeffizienten gegeben werden können, dann Neigungsfaktoren Linien werden gleich sein. Und umgekehrt: Wenn durch die Geradengleichungen mit gleichem Steigungskoeffizienten nicht zusammenfallende Geraden auf einer Ebene in einem rechtwinkligen Koordinatensystem gegeben sind, dann sind solche Geraden parallel.

Wenn die Linie a und die Linie b in einem rechtwinkligen Koordinatensystem die kanonischen Gleichungen der Linie auf der Ebene der Form definieren und , oder parametrische Gleichungen einer geraden Linie auf einer Ebene der Form und dann haben die Richtungsvektoren dieser Linien die Koordinaten und , und die Parallelitätsbedingung für die Linien a und b wird als geschrieben.

Schauen wir uns ein paar Beispiele an.

Beispiel.

Sind die Linien parallel? und ?

Lösung.

Wir schreiben die Gleichung einer geraden Linie in Segmenten in Form einer allgemeinen Gleichung einer geraden Linie um: . Jetzt können wir sehen, dass das der Normalenvektor der Geraden ist , und ist der Normalenvektor der Geraden. Diese Vektoren sind nicht kollinear, da es keine reelle Zahl t gibt, für die die Gleichheit ( ). Folglich ist die notwendige und hinreichende Bedingung für die Parallelität von Linien in der Ebene nicht erfüllt, daher sind die gegebenen Linien nicht parallel.

Antworten:

Nein, die Linien sind nicht parallel.

Beispiel.

Sind Geraden und Parallelen?

Lösung.

Wir bringen die kanonische Geradengleichung auf die Geradengleichung mit Steigung: . Offensichtlich sind die Gleichungen der Linien und nicht gleich (in diesem Fall wären die gegebenen Linien gleich) und die Steigungen der Linien sind gleich, daher sind die ursprünglichen Linien parallel.

Sie überschneiden sich nicht, egal wie lange sie andauern. Die Parallelität von Linien in der Schrift wird wie folgt angegeben: AB|| AUSE

Die Möglichkeit der Existenz solcher Linien wird durch einen Satz bewiesen.

Satz.

Durch jeden Punkt, der außerhalb einer gegebenen Linie liegt, kann man eine Parallele zu dieser Linie ziehen..

Lassen AB diese Zeile und AUS etwas außerhalb davon genommen. Das ist nachzuweisen AUS Sie können eine gerade Linie ziehen parallelAB. Lass uns weitermachen AB ab einem Punkt AUS aufrechtAUSD und dann werden wir AUSE^ AUSD, was ist möglich. Gerade CE parallel AB.

Für den Beweis nehmen wir das Gegenteil an, nämlich das CE schneidet AB irgendwann M. Dann ab dem Punkt M zu einer geraden Linie AUSD wir hätten zwei verschiedene Senkrechte MD und FRAU, was unmöglich ist. Meint, CE kann sich nicht überschneiden AB, d.h. AUSE parallel AB.

Folge.

Zwei Senkrechte (CEundDB) zu einer geraden Linie (СD) sind parallel.

Axiom der Parallelen.

Durch denselben Punkt ist es unmöglich, zwei verschiedene Linien parallel zu derselben Linie zu ziehen.

Also wenn eine gerade Linie AUSD, durch den Punkt gezogen AUS parallel zu einer Geraden AB, dann jede andere Zeile AUSE durch denselben Punkt AUS, kann nicht parallel sein AB, d.h. Sie macht weiter schneiden Mit AB.

Der Beweis dieser nicht ganz offensichtlichen Wahrheit erweist sich als unmöglich. Sie wird ohne Beweis als notwendige Annahme (Postulatum) akzeptiert.

Konsequenzen.

1. Wenn gerade(AUSE) schneidet sich mit einem von parallel(SW), dann schneidet es sich mit dem anderen ( AB), weil sonst durch denselben Punkt AUS zwei verschiedene gerade Linien, parallel AB, was unmöglich ist.

2. Wenn jeder der beiden Direkte (EINundB) sind parallel zu derselben dritten Linie ( AUS) , dann werden sie parallel untereinander.

In der Tat, wenn wir davon ausgehen EIN und B schneiden sich irgendwann M, dann würden zwei verschiedene, zueinander parallele Geraden durch diesen Punkt gehen. AUS, was unmöglich ist.

Satz.

Wenn ein Gerade ist senkrecht zu einer der parallelen Linien, dann steht sie senkrecht zur anderen parallel.

Lassen AB || AUSD und EF ^ AB.Das ist nachzuweisen EF ^ AUSD.

AufrechtEF, schneidend mit AB, wird sicherlich schneiden und AUSD. Der Schnittpunkt sei H.

Nehmen Sie jetzt an, dass AUSD nicht senkrecht dazu EH. Dann zum Beispiel eine andere Zeile HK, wird senkrecht zu sein EH und damit durch denselben Punkt H zwei gerade parallel AB: eines AUSD, nach Bedingung und die andere HK wie zuvor bewiesen. Da dies unmöglich ist, kann davon nicht ausgegangen werden SW war nicht senkrecht zu EH.

Zeichen der Parallelität zweier Linien

Satz 1. Wenn am Schnittpunkt zweier Sekanten gilt:

diagonal liegende Winkel sind gleich, oder

entsprechende Winkel gleich sind, oder

die Summe einseitiger Winkel beträgt dann 180°

Linien sind parallel(Abb. 1).

Nachweisen. Wir beschränken uns auf den Beweis von Fall 1.

Angenommen, am Schnittpunkt der Geraden a und b durch eine Sekante AB seien die quer liegenden Winkel gleich groß. Zum Beispiel ∠ 4 = ∠ 6. Lassen Sie uns beweisen, dass a || b.

Nehmen Sie an, dass die Linien a und b nicht parallel sind. Dann schneiden sie sich an einem Punkt M und folglich wird einer der Winkel 4 oder 6 der Außenwinkel des Dreiecks ABM sein. Sei der Deutlichkeit halber ∠ 4 die äußere Ecke des Dreiecks ABM und ∠ 6 die innere Ecke. Aus dem Satz über den Außenwinkel eines Dreiecks folgt, dass ∠ 4 größer als ∠ 6 ist, was der Bedingung widerspricht, dass sich die Geraden a und 6 nicht schneiden können, also parallel sind.

Folge 1. Zwei unterschiedliche Linien in einer Ebene senkrecht zu derselben Linie sind parallel(Abb. 2).

Kommentar. Die Art und Weise, wie wir gerade Fall 1 von Theorem 1 bewiesen haben, nennt man die Methode des Beweises durch Widerspruch oder Absurdität. Diese Methode hat ihren ersten Namen, weil zu Beginn der Argumentation eine Annahme gemacht wird, die dem entgegengesetzt ist, was bewiesen werden muss. Es wird Absurditätsreduktion genannt, weil wir auf der Grundlage der getroffenen Annahmen zu einer absurden Schlussfolgerung (Absurdität) kommen. Der Erhalt einer solchen Schlussfolgerung zwingt uns, die zu Beginn gemachte Annahme zu verwerfen und die zu akzeptieren, die bewiesen werden musste.

Aufgabe 1. Konstruiere eine Gerade, die durch einen gegebenen Punkt M und parallel zu einer gegebenen Geraden a verläuft, aber nicht durch den Punkt M verläuft.

Lösung. Wir ziehen eine Linie p durch den Punkt M senkrecht zur Linie a (Abb. 3).

Dann ziehen wir eine Linie b durch den Punkt M senkrecht zur Linie p. Die Linie b ist gemäß der Folgerung aus Satz 1 parallel zur Linie a.

Aus dem betrachteten Problem folgt eine wichtige Schlussfolgerung:
Durch einen Punkt, der nicht auf einer gegebenen Linie liegt, kann man immer eine Linie parallel zu der gegebenen Linie ziehen..

Die Haupteigenschaft paralleler Linien ist wie folgt.

Axiom der Parallelen. Durch einen gegebenen Punkt, der nicht auf einer gegebenen Linie liegt, gibt es nur eine Linie parallel zu der gegebenen Linie.

Betrachten Sie einige Eigenschaften paralleler Linien, die aus diesem Axiom folgen.

1) Wenn eine Linie eine der beiden parallelen Linien schneidet, dann schneidet sie die andere (Abb. 4).

2) Wenn zwei verschiedene Linien parallel zur dritten Linie sind, dann sind sie parallel (Abb. 5).

Auch der folgende Satz gilt.

Satz 2. Wenn zwei parallele Geraden von einer Sekante geschnitten werden, dann:

die Liegewinkel sind gleich;

entsprechende Winkel sind gleich;

die Summe einseitiger Winkel beträgt 180°.

Folge 2. Steht eine Gerade senkrecht auf einer von zwei parallelen Geraden, dann steht sie auch senkrecht auf der anderen.(siehe Abb.2).

Kommentar. Theorem 2 wird als Umkehrung von Theorem 1 bezeichnet. Die Konklusion von Theorem 1 ist die Bedingung von Theorem 2. Und die Bedingung von Theorem 1 ist die Konklusion von Theorem 2. Nicht jeder Theorem hat eine Inverse, d.h. wenn ein gegebener Theorem wahr ist, dann kann der Umkehrsatz falsch sein.

Erläutern wir dies am Beispiel des Satzes über vertikale Ecken. Dieser Satz kann wie folgt formuliert werden: Wenn zwei Winkel vertikal sind, dann sind sie gleich. Der umgekehrte Satz wäre folgender: Wenn zwei Winkel gleich sind, dann sind sie vertikal. Und das ist natürlich nicht wahr. Zwei gleiche Winkel muss nicht senkrecht sein.

Beispiel 1 Zwei parallele Linien werden von einer dritten gekreuzt. Es ist bekannt, dass die Differenz zwischen zwei einseitigen Innenwinkeln 30° beträgt. Finden Sie diese Winkel.

Lösung. Abbildung 6 soll die Bedingung erfüllen.

Ihre Privatsphäre ist uns wichtig. Aus diesem Grund haben wir eine Datenschutzrichtlinie entwickelt, die beschreibt, wie wir Ihre Informationen verwenden und speichern. Bitte lesen Sie unsere Datenschutzerklärung und lassen Sie uns wissen, wenn Sie Fragen haben.

Erhebung und Verwendung personenbezogener Daten

Personenbezogene Daten sind Daten, mit denen eine bestimmte Person identifiziert oder kontaktiert werden kann.

Sie können jederzeit um die Angabe Ihrer persönlichen Daten gebeten werden, wenn Sie uns kontaktieren.

Im Folgenden finden Sie einige Beispiele für die Arten von personenbezogenen Daten, die wir möglicherweise erfassen, und wie wir diese Daten möglicherweise verwenden.

Welche personenbezogenen Daten wir erheben:

• Wenn Sie eine Bewerbung auf der Website einreichen, erfassen wir möglicherweise verschiedene Informationen, einschließlich Ihres Namens, Ihrer Telefonnummer und Ihrer Adresse Email usw.

Wie wir Ihre personenbezogenen Daten verwenden:

• Die von uns gesammelten personenbezogenen Daten ermöglichen es uns, Sie zu kontaktieren und Sie über einzigartige Angebote, Werbeaktionen und andere Veranstaltungen und bevorstehende Veranstaltungen zu informieren.
• Von Zeit zu Zeit können wir Ihre personenbezogenen Daten verwenden, um Ihnen wichtige Mitteilungen und Mitteilungen zu senden.
• Wir können personenbezogene Daten auch für interne Zwecke verwenden, z. B. zur Durchführung von Audits, Datenanalysen und verschiedenen Recherchen, um die von uns angebotenen Dienstleistungen zu verbessern und Ihnen Empfehlungen zu unseren Dienstleistungen zu geben.
• Wenn Sie an einer Verlosung, einem Wettbewerb oder einem ähnlichen Anreiz teilnehmen, können wir die von Ihnen bereitgestellten Informationen verwenden, um solche Programme zu verwalten.

Weitergabe an Dritte

Wir geben die von Ihnen erhaltenen Informationen nicht an Dritte weiter.

Ausnahmen:

• Falls erforderlich - in Übereinstimmung mit dem Gesetz, einer gerichtlichen Anordnung, in Gerichtsverfahren und / oder aufgrund öffentlicher Anfragen oder Anfragen von Regierungsbehörden auf dem Territorium der Russischen Föderation - geben Sie Ihre persönlichen Daten preis. Wir können auch Informationen über Sie offenlegen, wenn wir feststellen, dass eine solche Offenlegung aus Gründen der Sicherheit, der Strafverfolgung oder aus anderen Gründen des öffentlichen Interesses notwendig oder angemessen ist.
• Im Falle einer Umstrukturierung, Fusion oder eines Verkaufs können wir die von uns erfassten personenbezogenen Daten an den entsprechenden Drittnachfolger übertragen.

Schutz personenbezogener Daten

Wir treffen Vorkehrungen – einschließlich administrativer, technischer und physischer – zum Schutz Ihrer personenbezogenen Daten vor Verlust, Diebstahl und Missbrauch sowie vor unbefugtem Zugriff, Offenlegung, Änderung und Zerstörung.

Wahrung Ihrer Privatsphäre auf Unternehmensebene

Um sicherzustellen, dass Ihre personenbezogenen Daten sicher sind, kommunizieren wir Datenschutz- und Sicherheitspraktiken an unsere Mitarbeiter und setzen Datenschutzpraktiken strikt durch.