( ichGut)

Mathematiklehrer PU №3

Tuaeva Z.S.

2015

Unterrichtsthema „Parallelität der Ebenen“

Unterrichtsart: Lektion im Erlernen von neuem Material.

Hauptziel:

Führen Sie das Konzept paralleler Ebenen ein.

Beweisen Sie ein Kriterium für die Parallelität zweier Ebenen.

Betrachten Sie die Eigenschaften paralleler Ebenen.

Aufgaben:

Lehrreich :

Die Fähigkeit entwickeln, das Zeichen der Parallelität zweier Ebenen und die untersuchten Eigenschaften paralleler Ebenen bei der Lösung von Problemen anzuwenden.

Lehrreich :

Entwicklung des räumlichen Vorstellungsvermögens der Schüler,

Entwicklung geistige Aktivität Studenten.

Entwicklung des logischen, rationalen, kritischen, kreativen Denkens und der kognitiven Fähigkeiten der Schüler.

Lehrreich :

Bildung von Genauigkeit, grafischen Fähigkeiten.

Verwendung von neu Bildungstechnologien: Nutzung der Technologie des Problemlernens.

Unterrichtsplan

Definition paralleler Ebenen.

Zeichen der Parallelität zweier Ebenen.

Eigenschaften paralleler Ebenen.

Ein Gespräch mit Schülern zu Themen, bei denen der Lehrer systematisch Problemsituationen schafft und die Aktivitäten der Schüler zur Lösung von Bildungsproblemen organisiert, gewährleistet die optimale Kombination ihrer unabhängigen Suchaktivitäten mit der Assimilation vorgefertigter Schlussfolgerungen der Wissenschaft.

III. Bildung von Fähigkeiten und Fertigkeiten

Lösen von Problemen für SchülerZeichen der Parallelität zweier Ebenen und Eigenschaften paralleler Ebenen. Selbstständige Arbeit um das Assimilierte zu kontrollieren und die primäre Konsolidierung des Materials durchzuführen

IV. Hausaufgaben

Der Lehrer kommentiert die Hausaufgaben

Während des Unterrichts:

1. Botschaft des Themas und Zwecks der Lektion. Nachricht zum Unterrichtsplan.

2. Die Phase der Wissensaktualisierung.

Fragen für Studierende:

1. Welche Linien im Raum nennt man parallel?

(Zwei Geraden im Raum heißen parallel, wenn sie in der gleichen Ebene liegen und keine gemeinsamen Punkte haben)

2. Formulieren Sie die Definition der Parallelität einer Geraden und einer Ebene?

(Eine Linie und eine Ebene heißen parallel, wenn sie keine gemeinsamen Punkte haben)

3. Formulieren Sie das dritte Axiom der Stereometrie?

(Wenn zwei Ebenen einen gemeinsamen Punkt haben, dann haben sie eine gemeinsame Linie, auf der alle gemeinsamen Punkte dieser Ebenen liegen)

4. Wie können zwei Ebenen im Raum lokalisiert werden?

(Zwei Ebenen schneiden sich entweder in einer geraden Linie (Abb. 1, a) oder schneiden sich nicht (Abb. 1, b))

Abb.1, a Abb.1, b

3. Neues Material lernen.

1. Lernproblem : Parallele Ebenen definieren.

Lernsituation :

Fragen für Studierende:

1. Wie viele gemeinsame Punkte haben zwei sich nicht schneidende Ebenen?

(Kein einziger gemeinsamer Punkt)

2. Wie heißen Ebenen, die keinen einzigen gemeinsamen Punkt haben?

(Parallele Ebenen)

3. Formulieren Sie die Definition paralleler Ebenen, gegeben die Anzahl ihrer gemeinsamen Punkte?

Zwei Ebenen heißen parallel, wenn sie keine gemeinsamen Punkte haben.

4. Geben Sie die Modelle paralleler Ebenen auf den Objekten des Klassenzimmers an?

(Schrankboden und -decke, zwei gegenüberliegende Wände, Tischfläche und Bodenebene)

2. Lernproblem : formulieren und beweisen Sie ein Parallelitätszeichen zweier Ebenen.

Lernsituation :

Die Schüler erhalten ein Modell eines Parallelepipeds.

Fragen für Studierende:

1. Wie ist die relative Position der Ebenen und ?

(Flugzeug und parallel)

2. Nennen Sie zwei sich schneidende Geraden

(gerade AB, gerade BC)

3. Benennen Sie die geraden Ebenen , parallel zu geraden LinienAB und Sonne ?

(
║
║

4. Wie ist die relative Position der geraden LinieAB und Flugzeug ? Begründen Sie die Antwort.

(AB║ aufgrund der Parallelität einer Geraden und einer Ebene: Wenn eine Gerade, die nicht in einer gegebenen Ebene liegt (
), ist parallel zu einer geraden Linie, die in dieser Ebene liegt (
║

Wenn es den Schülern schwer fällt, die Antwort zu begründen, lenken Sie ihre Aufmerksamkeit auf das Zeichen der Parallelität einer geraden Linie und einer Ebene.

5. Wie ist die relative Position der LinieSonne und Flugzeug ? Begründen Sie die Antwort.

(So║ aufgrund der Parallelität einer Geraden und einer Ebene: Wenn eine Gerade, die nicht in einer gegebenen Ebene liegt (
), ist parallel zu einer geraden Linie, die in dieser Ebene liegt (
║
), dann ist es parallel zur Ebene selbst)

6. Flugzeuge annehmen und sind nicht parallel. Wie werden sie sich dann befinden?

(die Ebenen schneiden sich entlang einer geraden Linie c)

7. Wie werden die Leitungen in diesem Fall angeordnet?AB undMit ?

(Mit ║AB, je nach Eigenschaft
) parallel zu einer anderen Ebene (AB║
║AB))

8. Wie werden die Leitungen in diesem Fall angeordnet?Sonne undMit ?

(Mit ║BC, je nach Eigenschaft : wenn das Flugzeug durch die gegebene Linie geht (
) parallel zu einer anderen Ebene (BC║ ) und schneidet diese Ebene (
), dann ist die Schnittlinie der Ebenen parallel zur gegebenen Linie (mit ║VS))

9. Wie viele Geraden sind parallel zu einer GeradenMit , geht durch den PunktBEI ?

(Zwei Linien: Linie AB, Linie BC)

10. Ist es möglich?

(Dies ist nicht möglich, weil nach dem Satz über Parallelen: Durch jeden Punkt im Raum, der nicht auf einer gegebenen Geraden liegt, verläuft eine Gerade parallel zu der gegebenen, und zwar nur eine)

11. Welche Schlussfolgerung lässt sich ziehen? Ist unsere Annahme richtig?

(Unsere Annahme ist nicht richtig, das bleibt zuzugeben ║)

12. Wie viele Geraden braucht man in einer Ebene zu planieren und waren parallel?

(zwei gerade Linien)

13. Was sollen diese Linien untereinander sein?

(sich kreuzen)

14. Wie viele gerade Linien müssen parallel zur Ebene sein? ?

(Zwei)

15. Formulieren Sie ein Zeichen der Parallelität zweier Ebenen unter Berücksichtigung der Anzahl der Linien einer Ebene parallel zu den Linien einer anderen Ebene?

Das Ergebnis der Schlussfolgerung der Studenten:

Wenn zwei sich schneidende Geraden einer Ebene jeweils parallel zu zwei Geraden einer anderen Ebene sind, dann sind diese Ebenen parallel.

3. Lernproblem : formulieren und beweisen Sie die Eigenschaften paralleler Ebenen.

Lernsituation :

Fragen für Studierende:

und ?

(Ebenen sind parallel)

in Bezug auf Flugzeuge und ?

(Flugzeug durchquert das Flugzeug und )

3. Was können Sie über die Schnittlinien der Ebenen sagen?

(die Schnittlinien der Ebenen sind parallel zueinander)

4. Begründen Sie Ihre Antwort anhand der Definition paralleler Linien im Raum.

(Linien a und b liegen in der gleichen Ebene) und schneiden sich nicht, denn wenn sich die Linien schneiden, dann die Ebenen und einen gemeinsamen Punkt haben, was unmöglich ist, da diese Ebenen parallel sind)

5. Formulieren Sie die erste Eigenschaft paralleler Ebenen unter Berücksichtigung der relativen Lage der Schnittliniena und in ?

Das Ergebnis der Schlussfolgerung der Studenten:

Wenn zwei parallele Ebenen von einer dritten geschnitten werden, dann sind ihre Schnittlinien parallel.

Lernsituation :

Den Schülern wird ein Modell aus parallelen Ebenen gegeben, die von einer dritten Ebene geschnitten werden.

Fragen für Studierende:

1. Wie ist die relative Position der Ebenen und ?

(Ebenen sind parallel)

2. Wie sich das Flugzeug befindet in Bezug auf Flugzeuge und ?

(Flugzeug durchquert das Flugzeug und )

3. Was können Sie über Segmente sagen?AB und AUS D ?

(Segmente Eine Band AUS D parallel zueinander)

4. Was können Sie über Segmente sagen?AC und BEI D ?

(Segmente AU und BEI D sind nach Eigenschaft 1 parallel zueinander )

5. Wie heißt ein Viereck, dessen gegenüberliegende Seiten paarweise parallel sind?

(Parallelogramm)

6. Welche Eigenschaften eines Parallelogramms kennst du?

In einem Parallelogramm sind gegenüberliegende Seiten und Winkel gleich

Die Diagonalen eines Parallelogramms werden durch den Schnittpunkt halbiert

7. Was können Sie über Segmente sagen?AB und AUS D mit der ersten Eigenschaft eines Parallelogramms?

(Segmente Eine Band AUS D untereinander gleich)

8. Formulieren Sie die zweite Eigenschaft paralleler Ebenen mit Hilfe der StreckengleichheitAB und AUS D ?

Das Ergebnis der Schlussfolgerung der Studenten:

Segmente paralleler Linien, die zwischen parallelen Ebenen eingeschlossen sind, sind gleich.

4. Bildung von Fähigkeiten und Fertigkeiten.

Probleme lösen

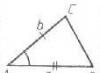
Aufgabe Nummer 1. (Nr. 54) (Ermitteln des Zeichens der Parallelität zweier Ebenen)

Gegeben :

Beweisen :

║

Finden :

Nachweisen:

1.
- Mittellinie
MN ║ AC .

2. NP - Mittellinie
NP ║ CD .

MN ║ AC
( MNP )║( ADC ) auf der Basis von Parallelität 2 pl.

NP ║ CD

4.
ähnlich
gemäß dem dritten Zeichen der Ähnlichkeit von Dreiecken (wenn drei Seiten eines Dreiecks proportional zu drei Seiten eines anderen sind, dann sind solche Dreiecke ähnlich)
(da das Verhältnis der Flächen zweier ähnlicher Dreiecke gleich dem Quadrat des Ähnlichkeitskoeffizienten ist)

Antworten :
.

Aufgabe Nummer 2. (Nr. 63 (a)) (Zum Erarbeiten von 1 Eigenschaften paralleler Ebenen)

Gegeben:

║

Finden:

Lösung:

1. Lassen Sie uns das beweisen
║
.

Als

║(nach Zustand)

║
.(durch 1 Eigenschaft paralleler Ebenen)

2. Lassen Sie uns das beweisen
ähnlich
.

, wie entsprechend bei
║
.und Sekante

, wie entsprechend bei
║
.und Sekante

Meint,
ähnlich
an 2 Ecken.

3. Finden
.

Nach Zustand

4. Finden
.

Machen wir eine Proportion:

Antworten :

Aufgabe Nummer 3. (Nr. 65) (Zum Üben von 2 Eigenschaften paralleler Ebenen)

Gegeben :

║

║
║

Definieren :

Art von Vierecken

Beweisen:

Lösung:

1. Betrachten Sie ein Viereck
.

║
(nach Zustand)

=

Viereck

2. Betrachten Sie ein Viereck
.

║
(nach Zustand)

=
(als Segmente paralleler Linien, die zwischen parallelen Ebenen eingeschlossen sind, Eigenschaft 2)
Viereck
ist ein Parallelogramm

3. Betrachten Sie ein Viereck
.

║
(nach Zustand)

=
(als Segmente paralleler Linien, die zwischen parallelen Ebenen eingeschlossen sind, Eigenschaft 2)
Viereck
schneidet ein ähnliches Dreieck wie das gegebene ab. : ║ Hausaufgaben.

§ 10 (S. 10-11) S. (20-21)

Nr. 53, Nr. 63(b).

Lehrbuch: L. S. Atanasyan, V. F. Butuzov, S. B. Kadomtsev, L. S. Kiseleva, E. G. Poznyak. Geometrie 10, 11. Moskau“ Ausbildung ” , 2002.

6. Das Ergebnis der Lektion.

Heute haben wir in der Lektion das Konzept paralleler Ebenen eingeführt, das Zeichen der Parallelität zweier Ebenen unabhängig voneinander bewiesen und die Eigenschaften paralleler Ebenen berücksichtigt. Wir haben gelernt, Beweisprobleme mit dem Zeichen der Parallelität zweier Ebenen zu lösen und die untersuchten Eigenschaften paralleler Ebenen bei der Lösung von Problemen anzuwenden.

Unterrichtsziele:

• Führen Sie das Konzept paralleler Ebenen ein.
• Betrachten und beweisen Sie Sätze, die das Zeichen der Parallelität von Ebenen und die Eigenschaften paralleler Ebenen ausdrücken.
• Befolgen Sie die Anwendung dieser Theoreme beim Lösen von Problemen.

Stundenplan (an die Tafel schreiben):

I. Vorbereitende mündliche Arbeit.

II. Neues lernen:

1. Gegenseitiges Einverständnis zwei Flugzeuge im Weltraum.
2. Definition paralleler Ebenen.
3. Zeichen paralleler Ebenen.
4. Eigenschaft paralleler Ebenen.

III. Zusammenfassung der Lektion.

IV. Hausaufgaben.

WÄHREND DER KLASSEN

I. Mündliche Arbeit

Ich möchte die Lektion mit einem Zitat aus Chaadaevs philosophischem Brief beginnen:

„Woher kommt diese wundersame Kraft der Analyse in der Mathematik? Tatsache ist, dass der Geist hier in völligem Gehorsam gegenüber dieser Regel arbeitet.

Wir werden diese Unterordnung unter die Regel in der nächsten Aufgabe betrachten. Um neues Material aufzunehmen, müssen einige Fragen wiederholt werden. Dazu müssen Sie aus diesen Aussagen eine Aussage aufstellen und Ihre Antwort begründen:

II. Neues Material lernen

1. Wie können zwei Ebenen im Raum lokalisiert werden? Was ist die Menge der Punkte, die zu beiden Ebenen gehören?

Antworten:

a) zusammenfallen (dann werden wir uns mit einem Flugzeug befassen, nicht zufrieden);
b) schneiden, ;
c) sich nicht schneiden (es gibt überhaupt keine gemeinsamen Punkte).

2. Definition: Wenn sich zwei Ebenen nicht schneiden, werden sie als parallel bezeichnet.

3. Bezeichnung:

4. Nennen Sie Beispiele für parallele Ebenen aus der Umgebung

5. Wie findet man heraus, ob zwei beliebige Ebenen im Raum parallel sind?

Antworten:

Sie können die Definition verwenden, aber das ist nicht praktikabel, weil Es ist nicht immer möglich, den Schnittpunkt von Ebenen festzulegen. Daher ist es notwendig, eine Bedingung zu berücksichtigen, die ausreicht, um die Parallelität der Ebenen zu bestätigen.

6. Betrachten Sie Situationen:

b) wenn ?

c) wenn ?

Warum lautet die Antwort bei a) und b) „nicht immer“, aber bei c) „ja“? (Schnittlinien definieren eine Ebene eindeutig, sind also eindeutig definiert!)

Situation 3 ist ein Zeichen für Parallelität zweier Ebenen.

7. Satz: Wenn zwei sich schneidende Geraden einer Ebene jeweils parallel zu zwei Geraden einer anderen Ebene sind, dann sind diese Ebenen parallel.

Gegeben:

Beweisen:

Nachweisen:

(Notationen auf der Zeichnung werden von den Schülern angebracht).

1. Hinweis: . Ähnlich:
2. Lassen Sie: .
3. Wir haben: Ähnlich:
4. Wir erhalten: Ein Widerspruch mit dem Axiom der Planimetrie geht durch M.
5. Also: falsch, dann h. usw.

8. Lösen Sie Nr. 51 (Schüler bringen Bezeichnungen auf der Zeichnung an).

Gegeben:

Beweisen:

Nachweisen:

1 Weg

1. Lass uns bauen

2-Wege

Geben Sie über über ein.

9. Betrachten Sie zwei Eigenschaften paralleler Ebenen:

Satz: Wenn zwei parallele Ebenen von einer dritten geschnitten werden, dann sind ihre Schnittlinien parallel.

(Schüler selbst vervollständigen und markieren die Zeichnung).

Gegeben:

In diesem Artikel werden die Probleme der Parallelität von Ebenen untersucht. Lassen Sie uns eine Definition von Ebenen geben, die parallel zueinander sind; wir bezeichnen die Zeichen und hinreichenden Bedingungen der Parallelität; Betrachten wir die Theorie anhand von Illustrationen und praktischen Beispielen.

Yandex.RTB R-A-339285-1 Definition 1

Parallele Ebenen sind Ebenen, die keine gemeinsamen Punkte haben.

Zur Bezeichnung der Parallelität wird das folgende Symbol verwendet: ∥. Wenn zwei Ebenen gegeben sind: α und β , die parallel sind, sieht eine kurze Aufzeichnung darüber so aus: α ‖ β .

In der Zeichnung werden in der Regel zueinander parallele Ebenen als zwei dargestellt gleiches Parallelogramm die gegeneinander versetzt sind.

In der Sprache kann Parallelität wie folgt bezeichnet werden: Die Ebenen α und β sind parallel, und auch - die Ebene α ist parallel zur Ebene β oder die Ebene β ist parallel zur Ebene α.

Parallelität der Ebenen: Zeichen und Bedingungen der Parallelität

Im Entscheidungsprozess geometrische Probleme oft stellt sich die frage: sind die gegebenen ebenen parallel zueinander? Zur Beantwortung dieser Frage wird das Zeichen der Parallelität verwendet, das auch eine hinreichende Bedingung für die Parallelität der Ebenen ist. Schreiben wir es als Theorem auf.

Satz 1

Ebenen sind parallel, wenn zwei Schnittgeraden einer Ebene jeweils parallel zu zwei Schnittgeraden einer anderen Ebene sind.

Der Beweis dieses Satzes wird im Geometrieprogramm für die Klassen 10 - 11 gegeben.

In der Praxis werden zum Beweis der Parallelität unter anderem die folgenden beiden Theoreme verwendet.

Satz 2

Wenn eine der parallelen Ebenen parallel zur dritten Ebene ist, dann ist die andere Ebene entweder ebenfalls parallel zu dieser Ebene oder fällt mit ihr zusammen.

Satz 3

Wenn zwei nicht zusammenfallende Ebenen senkrecht zu einer Linie stehen, dann sind sie parallel.

Auf der Grundlage dieser Sätze und des Zeichens der Parallelität selbst ist die Tatsache der Parallelität zweier beliebiger Ebenen bewiesen.

Betrachten wir genauer die notwendige und hinreichende Bedingung für die Parallelität der Ebenen α und β, gegeben in einem rechtwinkligen Koordinatensystem des dreidimensionalen Raums.

Nehmen wir an, dass in einem rechtwinkligen Koordinatensystem die Ebene α gegeben ist, die der allgemeinen Gleichung A 1 x + B 1 y + C 1 z + D 1 = 0 entspricht, und auch die Ebene β gegeben ist, die durch definiert ist die allgemeine Gleichung der Form A 2 x + B 2 y + C 2 z + D 2 = 0 .

Satz 4

Damit die gegebenen Ebenen α und β parallel sind, ist es notwendig und ausreichend, dass das System lineare Gleichungen A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 hatte keine Lösung (war widersprüchlich).

Nachweisen

Angenommen, die durch die Gleichungen A 1 x + B 1 y + C 1 z + D 1 = 0 und A 2 x + B 2 y + C 2 z + D 2 = 0 definierten Ebenen sind parallel und haben daher keine gemeinsame Punkte. Es gibt also keinen einzigen Punkt im rechtwinkligen Koordinatensystem des dreidimensionalen Raums, dessen Koordinaten gleichzeitig den Bedingungen beider Ebenengleichungen entsprechen würden, d.h. System A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 hat keine Lösung. Wenn das angegebene System keine Lösungen hat, dann gibt es im rechtwinkligen Koordinatensystem des dreidimensionalen Raums keinen einzigen Punkt, dessen Koordinaten gleichzeitig die Bedingungen beider Gleichungen des Systems erfüllen würden. Daher haben die durch die Gleichungen A 1 x + B 1 y + C 1 z + D 1 = 0 und A 2 x + B 2 y + C 2 z + D 2 = 0 gegebenen Ebenen keine gemeinsamen Punkte, d.h. sie sind parallel.

Analysieren wir die Verwendung der notwendigen und hinreichenden Bedingung für die Parallelität der Ebenen.

Beispiel 1

Gegeben seien zwei Ebenen: 2 x + 3 y + z - 1 = 0 und 2 3 x + y + 1 3 z + 4 = 0 . Sie müssen feststellen, ob sie parallel sind.

Lösung

Wir schreiben das Gleichungssystem aus den gegebenen Bedingungen auf:

2 x + 3 y + z - 1 = 0 2 3 x + y + 1 3 z + 4 = 0

Prüfen wir, ob es möglich ist, das resultierende lineare Gleichungssystem zu lösen.

Der Rang der Matrix 2 3 1 2 3 1 1 3 ist gleich eins, da die Minoren zweiter Ordnung gleich null sind. Der Rang der Matrix 2 3 1 1 2 3 1 1 3 - 4 ist gleich zwei, da der Minor von 2 1 2 3 - 4 nicht Null ist. Somit ist der Rang der Hauptmatrix des Gleichungssystems kleiner als der Rang der erweiterten Matrix des Systems.

Zusammen damit folgt aus dem Satz von Kronecker-Capelli: Das Gleichungssystem 2 x + 3 y + z - 1 = 0 2 3 x + y + 1 3 z + 4 = 0 hat keine Lösungen. Diese Tatsache beweist, dass die Ebenen 2 x + 3 y + z - 1 = 0 und 2 3 x + y + 1 3 z + 4 = 0 parallel sind.

Beachten Sie, dass die Anwendung der Gauß-Methode zur Lösung eines Systems linearer Gleichungen dasselbe Ergebnis liefern würde.

Antworten: gegebene Ebenen sind parallel.

Die notwendige und hinreichende Bedingung für die Parallelität der Ebenen kann auch anders beschrieben werden.

Satz 5

Damit zwei nicht zusammenfallende Ebenen α und β parallel zueinander sind, ist es notwendig und ausreichend, dass die Normalenvektoren der Ebenen α und β kollinear sind.

Der Beweis der formulierten Bedingung basiert auf der Definition des Normalenvektors der Ebene.

Angenommen, dass n 1 → = (A 1 , B 1 , C 1 ) und n 2 → = (A 2 , B 2 , C 2 ) die Normalenvektoren der Ebenen α bzw. β sind. Schreiben wir die Bedingung der Kollinearität dieser Vektoren:

n 1 → = t n 2 ⇀ ⇔ A 1 = t A 2 B 1 = t B 2 C 1 = t C 2, wobei t eine reelle Zahl ist.

Damit die nicht zusammenfallenden Ebenen α und β mit den oben angegebenen Normalenvektoren parallel sind, ist es also notwendig und ausreichend, dass eine reelle Zahl t auftritt, für die die Gleichheit gilt:

n 1 → = t n 2 ⇀ ⇔ EIN 1 = t EIN 2 B 1 = t B 2 C 1 = t C 2

Beispiel 2

Die Ebenen α und β sind in einem rechtwinkligen Koordinatensystem des dreidimensionalen Raums gegeben. Die Ebene α geht durch die Punkte: A (0 , 1 , 0) , B (- 3 , 1 , 1) , C (- 2 , 2 , - 2) . Die Ebene β wird durch die Gleichung x 12 + y 3 2 + z 4 = 1 beschrieben. Es ist notwendig, die Parallelität der gegebenen Ebenen zu beweisen.

Lösung

Stellen wir sicher, dass die angegebenen Ebenen nicht zusammenfallen. In der Tat, denn die Koordinaten des Punktes A entsprechen nicht der Ebenengleichung β.

Der nächste Schritt besteht darin, die Koordinaten der Normalenvektoren n 1 → und n 2 → zu bestimmen, die den Ebenen α und β entsprechen. Wir prüfen auch die Bedingung der Kollinearität dieser Vektoren.

Der Vektor n 1 → kann durch Bilden des Kreuzprodukts von Vektoren spezifiziert werden A B → und Ein C → . Ihre Koordinaten sind jeweils: (- 3 , 0 , 1) und (- 2 , 2 , - 2) . Dann:

n 1 → = A B → × A C → = i → j → k → - 3 0 1 - 2 1 - 2 = - i → - 8 j → - 3 k → ⇔ n 1 → = (- 1 , - 8 , - 3)

Um die Koordinaten des Normalenvektors der Ebene x 12 + y 3 2 + z 4 = 1 zu erhalten, reduzieren wir diese Gleichung auf die allgemeine Ebenengleichung:

x 12 + y 3 2 + z 4 = 1 ⇔ 1 12 x + 2 3 y + 1 4 z - 1 = 0

Also: n 2 → = 1 12 , 2 3 , 1 4 .

Prüfen wir, ob die Bedingung der Kollarität der Vektoren n 1 → = (- 1 , - 8 , - 3) und n 2 → = 1 12 , 2 3 , 1 4 ist

Da - 1 \u003d t 1 12 - 8 \u003d t 2 3 - 3 \u003d t 1 4 ⇔ t \u003d - 12, sind die Vektoren n 1 → und n 2 → durch die Gleichheit n 1 → = - 12 verbunden n 2 → , d.h. sind kollinear.

Antworten: Ebenen α und β fallen nicht zusammen; ihre Normalenvektoren sind kollinear. Somit sind die Ebenen α und β parallel.

Wenn Sie einen Fehler im Text bemerken, markieren Sie ihn bitte und drücken Sie Strg+Enter

Jeder, der jemals studiert hat oder derzeit eine Schule besucht, musste sich verschiedenen Schwierigkeiten beim Studium der Disziplinen stellen, die in dem vom Bildungsministerium entwickelten Programm enthalten sind.

Welchen Schwierigkeiten begegnen Sie

Das Erlernen von Sprachen wird begleitet vom Auswendiglernen bestehender grammatikalischer Regeln und der wichtigsten Ausnahmen davon. Der Sportunterricht erfordert von den Schülern eine große Berechnung, eine gute körperliche Verfassung und große Geduld.

Nichts ist jedoch vergleichbar mit den Schwierigkeiten, die beim Studium exakter Disziplinen auftreten. Algebra, die komplizierte Wege zur Lösung elementarer Probleme enthält. Physik mit einem reichen Formelsatz für physikalische Gesetze. Geometrie und ihre Abschnitte, die auf komplexen Sätzen und Axiomen beruhen.

Ein Beispiel sind die Axiome, die die Theorie der Parallelität von Ebenen erklären, an die man sich erinnern muss, da sie dem gesamten Kurs des Schullehrplans über Stereometrie zugrunde liegen. Versuchen wir herauszufinden, wie einfacher und schneller dies möglich ist.

Parallele Ebenen durch Beispiele

Das Axiom, das die Parallelität der Ebenen angibt, lautet wie folgt: " Zwei beliebige Ebenen gelten nur dann als parallel, wenn sie keine gemeinsamen Punkte enthalten.“, das heißt, sie überschneiden sich nicht. Um sich dieses Bild genauer vorzustellen, wie elementares Beispiel Sie können das Verhältnis von Decke und Boden oder gegenüberliegenden Wänden in das Gebäude bringen. Es wird sofort klar, was gemeint ist, und es bestätigt sich auch die Tatsache, dass sich diese Ebenen im Normalfall niemals schneiden werden.

Ein weiteres Beispiel ist ein doppelt verglastes Fenster, bei dem Glasscheiben als Ebenen wirken. Sie werden auch keinesfalls Schnittpunkte miteinander bilden. Darüber hinaus können Sie Bücherregale, einen Zauberwürfel, bei dem die Flugzeuge die gegenüberliegenden Seiten sind, und andere Elemente des täglichen Lebens hinzufügen.

Die betrachteten Ebenen sind mit einem Sonderzeichen in Form von zwei Geraden „||“ gekennzeichnet, die die Parallelität der Ebenen deutlich machen. Also Bewerbung echte Beispiele, können Sie sich eine klarere Wahrnehmung des Themas bilden und können daher zur Betrachtung komplexerer Konzepte übergehen.

Wo und wie wird die Theorie der parallelen Ebenen angewendet?

Beim Lernen Schulkurs Geometrie haben die Studierenden vielseitige Aufgaben zu bewältigen, bei denen es oft erforderlich ist, die Parallelität von Linien, Geraden und Ebenen untereinander oder die Abhängigkeit von Ebenen voneinander zu bestimmen. Durch die Analyse des bestehenden Zustands kann jede Aufgabe den vier Hauptklassen der Stereometrie zugeordnet werden.

Die erste Klasse umfasst Aufgaben, bei denen es notwendig ist, die Parallelität einer geraden Linie und einer Ebene zwischen sich zu bestimmen. Seine Lösung reduziert sich auf den Beweis des gleichnamigen Satzes. Dazu müssen Sie feststellen, ob zu einer Geraden, die nicht zur betrachteten Ebene gehört, eine parallele Gerade in dieser Ebene liegt.

Die zweite Klasse von Problemen umfasst diejenigen, bei denen das Zeichen paralleler Ebenen verwendet wird. Es wird verwendet, um den Beweisprozess zu vereinfachen und dadurch die Zeit für die Lösungsfindung erheblich zu verkürzen.

Die nächste Klasse behandelt das Spektrum der Probleme zur Zuordnung von Linien zu den Haupteigenschaften der Parallelität von Ebenen. Die Lösung von Problemen der vierten Klasse besteht darin, festzustellen, ob die Bedingung paralleler Ebenen erfüllt ist. Wenn Sie genau wissen, wie der Beweis eines bestimmten Problems erfolgt, können sich die Schüler leichter zurechtfinden, wenn sie das vorhandene Arsenal geometrischer Axiome anwenden.

Somit werden die Probleme, deren Bedingung es erfordert, die Parallelität von geraden Linien, einer geraden Linie und einer Ebene oder zwei Ebenen untereinander zu definieren und zu beweisen, reduziert auf richtige Auswahl Sätze und Lösung nach dem bestehenden Regelwerk.

Über die Parallelität einer Geraden und einer Ebene

Die Parallelität einer Linie und einer Ebene ist ein spezielles Thema in der Stereometrie, da es genau darum geht Basiskonzept, auf der alle nachfolgenden Eigenschaften der Parallelität geometrischer Figuren beruhen.

Wenn zwei Punkte einer Geraden zu einer bestimmten Ebene gehören, können wir nach den verfügbaren Axiomen schließen, dass die gegebene Gerade auch in ihr liegt. In dieser Situation wird deutlich, dass es drei Möglichkeiten für die Lage der Linie relativ zur Ebene im Raum gibt:

1. Die Linie gehört zum Flugzeug.
2. Für eine Linie und eine Ebene gibt es einen gemeinsamen Schnittpunkt.
3. Es gibt keine Schnittpunkte für eine Gerade und eine Ebene.

Uns interessiert vor allem die letzte Variante, wenn es keine Schnittpunkte gibt. Nur dann können wir sagen, dass die Linie und die Ebene relativ zueinander parallel sind. Somit wird die Bedingung des Hauptsatzes über das Zeichen der Parallelität einer Geraden und einer Ebene bestätigt, die besagt, dass: "Wenn eine Linie, die nicht zur fraglichen Ebene gehört, parallel zu einer Linie in dieser Ebene ist, dann ist die fragliche Linie auch parallel zu der gegebenen Ebene."

Die Notwendigkeit, das Zeichen der Parallelität zu verwenden

Das Zeichen der Parallelität von Ebenen wird normalerweise verwendet, um eine vereinfachte Lösung von Problemen mit Ebenen zu finden. Wesen dieses Schild ist wie folgt: " Liegen zwei sich schneidende Geraden in derselben Ebene parallel zu zwei Geraden einer anderen Ebene, so können solche Ebenen als parallel bezeichnet werden».

Zusätzliche Theoreme

Zusätzlich zur Verwendung eines Merkmals, das die Parallelität von Ebenen beweist, kann man in der Praxis auf die Verwendung von zwei weiteren zusätzlichen Theoremen stoßen. Der erste wird in vorgestellt folgendes Formular: « Wenn eine der beiden parallelen Ebenen parallel zur dritten ist, dann ist die zweite Ebene entweder auch parallel zur dritten oder fällt vollständig mit ihr zusammen».

Aufgrund der Verwendung der gegebenen Theoreme ist es immer möglich, die Parallelität der Ebenen in Bezug auf den betrachteten Raum zu beweisen. Der zweite Satz zeigt die Abhängigkeit von Ebenen von einer senkrechten Linie und hat die Form: „ Wenn zwei nicht zusammenfallende Ebenen senkrecht zu einer geraden Linie stehen, werden sie als parallel zueinander betrachtet».

Das Konzept einer notwendigen und hinreichenden Bedingung

Beim wiederholten Lösen von Problemen zum Beweis der Parallelität von Ebenen wurde eine notwendige und hinreichende Bedingung für die Parallelität von Ebenen hergeleitet. Es ist bekannt, dass jede Ebene durch eine parametrische Gleichung der Form gegeben ist: A 1 x+ B 1 y+ C 1 z+D 1 =0. Unsere Bedingung basiert auf der Verwendung eines Gleichungssystems, das die Lage von Ebenen im Raum angibt, und wird durch die folgende Formulierung dargestellt: Um die Parallelität zweier Ebenen zu beweisen, ist es notwendig und ausreichend, dass das Gleichungssystem, das diese Ebenen beschreibt, inkonsistent ist, dh keine Lösung hat».

Grundeigenschaften

Bei der Lösung geometrischer Probleme reicht es jedoch nicht immer aus, das Zeichen der Parallelität zu verwenden. Manchmal tritt eine Situation auf, in der die Parallelität von zwei oder mehr Linien in verschiedenen Ebenen oder die Gleichheit der auf diesen Linien enthaltenen Segmente nachgewiesen werden muss. Nutzen Sie dazu die Eigenschaften paralleler Ebenen. In der Geometrie gibt es nur zwei davon.

Die erste Eigenschaft ermöglicht es Ihnen, die Parallelität von Linien in bestimmten Ebenen zu beurteilen und wird in dargestellt folgendes Formular: « Wenn zwei parallele Ebenen von einer dritten geschnitten werden, dann sind auch die durch die Schnittlinien gebildeten Linien parallel zueinander».

Die Bedeutung der zweiten Eigenschaft besteht darin, die Gleichheit von Segmenten zu beweisen, die auf parallelen Linien liegen. Ihre Interpretation wird im Folgenden vorgestellt. " Wenn wir zwei parallele Ebenen betrachten und zwischen ihnen einen Bereich einschließen, kann argumentiert werden, dass die Länge der von diesem Bereich gebildeten Segmente gleich ist».

In dieser Lektion werden wir drei Eigenschaften paralleler Ebenen betrachten: den Schnittpunkt zweier paralleler Ebenen mit einer dritten Ebene; um parallele Segmente eingeschlossen zwischen parallelen Ebenen; und über das Schneiden der Seiten eines Winkels durch parallele Ebenen. Als Nächstes werden wir mithilfe dieser Eigenschaften mehrere Probleme lösen.

Thema: Parallelität von Linien und Ebenen

Lektion: Eigenschaften paralleler Ebenen

Wenn zwei parallele Ebenen von einer dritten geschnitten werden, dann sind ihre Schnittlinien parallel.

Nachweisen

Seien parallele Ebenen und und eine Ebene gegeben, die die Ebenen und entlang gerader Linien schneidet a und b(Abb. 1.).

Direkte a und b liegen in der gleichen Ebene, nämlich in der γ-Ebene. Lassen Sie uns beweisen, dass die Linien a und b nicht schneiden.

Wenn direkt a und b schneiden, das heißt, einen gemeinsamen Punkt haben würden, dann würde dieser gemeinsame Punkt zu zwei Ebenen und , und gehören, was unmöglich ist, da sie aufgrund der Bedingung parallel sind.

Also gerade a und b parallel, was zu beweisen war.

Segmente paralleler Linien, die zwischen parallelen Ebenen eingeschlossen sind, sind gleich.

Nachweisen

Gegeben seien parallele Ebenen und parallele Geraden AB und AUSD die diese Ebenen schneiden (Abb. 2.). Lassen Sie uns beweisen, dass die Segmente AB und AUSD sind gleich.

Zwei parallele Linien AB und AUSD bilden eine einzige Ebene γ, γ = ABDAUS. Die Ebene γ schneidet parallele Ebenen und entlang paralleler Linien (nach der ersten Eigenschaft). Also gerade AC und BEID sind parallel.

Direkte AB und AUSD sind ebenfalls parallel (durch Bedingung). Also das Viereck ABDAUS ist ein Parallelogramm, weil seine gegenüberliegenden Seiten parallel sind.

Aus den Eigenschaften eines Parallelogramms folgt, dass die Segmente AB und AUSD gleich sind, was zu beweisen war.

Parallele Ebenen schneiden die Seiten des Winkels in proportionale Teile.

Nachweisen

Gegeben seien parallele Ebenen, die die Seiten des Winkels schneiden ABER(Abb. 3.). Das müssen wir beweisen.

Parallele Ebenen und geschnitten durch die Winkelebene ABER. Nennen wir die Schnittlinie der Winkelebene ABER und Flugzeuge - Sonne, und die Schnittlinie der Ebene des Winkels ABER und Flugzeuge - B 1 ab 1. Gemäß der ersten Eigenschaft sind die Schnittlinien Sonne und B 1 ab 1 sind parallel.

Also die Dreiecke ABC und AB 1 C 1 sind ähnlich. Wir bekommen:

3. Mathematische Website von Tsegelny Vitaly Stanislavovich ()

4. Festival der pädagogischen Ideen "Offener Unterricht" ()

1 Punkt Ö- gemeinsamer Mittelpunkt jedes Segments AA1, BB1, SS1 die nicht in der gleichen Ebene liegen. Beweisen Sie, dass Flugzeuge ABC und A 1 B 1 C 1 sind parallel.

2. Beweisen Sie, dass es möglich ist, parallele Ebenen durch zwei sich schneidende Geraden zu zeichnen.

3. Beweisen Sie, dass eine Gerade, die eine von zwei parallelen Ebenen schneidet, auch die andere schneidet.

4. Geometrie. Klasse 10-11: ein Lehrbuch für Schüler von Bildungseinrichtungen (Grund- und Profilniveau) / I. M. Smirnova, V. A. Smirnov. - 5. Auflage, korrigiert und ergänzt - M.: Mnemozina, 2008. - 288 S.: mit Abb.

Aufgaben 6, 8, 9 Seite 29