Die Formel für das Volumen eines Prismas. Das Volumen eines dreieckigen Prismas: eine allgemeine Typformel und eine Formel für ein reguläres Prisma

Der Videokurs "Get an A" beinhaltet alle Themen, die für das erfolgreiche Bestehen der Prüfung in Mathematik mit 60-65 Punkten notwendig sind. Erledigen Sie alle Aufgaben 1-13 des Profils USE in Mathematik. Auch zum Bestehen der Basic USE in Mathematik geeignet. Wer die Prüfung mit 90-100 Punkten bestehen will, muss Teil 1 in 30 Minuten und ohne Fehler lösen!

Prüfungsvorbereitungskurs für die Klassen 10-11, sowie für Lehrkräfte. Alles, was Sie brauchen, um Teil 1 der Prüfung in Mathematik (die ersten 12 Aufgaben) und Aufgabe 13 (Trigonometrie) zu lösen. Und das sind mehr als 70 Punkte im Einheitlichen Staatsexamen, und darauf kann weder ein Hundertpunkte-Student noch ein Humanist verzichten.

Die ganze notwendige Theorie. Schnelle Wege Lösungen, Fallen und Geheimnisse der Prüfung. Alle relevanten Aufgaben von Teil 1 der Bank of FIPI-Aufgaben wurden analysiert. Der Kurs entspricht vollständig den Anforderungen des USE-2018.

Der Kurs beinhaltet 5 große Themen zu je 2,5 Stunden. Jedes Thema ist von Grund auf neu, einfach und übersichtlich.

Hunderte von Prüfungsaufgaben. Textprobleme und Wahrscheinlichkeitstheorie. Einfache und leicht zu merkende Problemlösungsalgorithmen. Geometrie. Theorie, Referenzmaterial, Analyse aller Arten von USE-Aufgaben. Stereometrie. Knifflige Tricks Lösungen, nützliche Spickzettel, Entwicklung des räumlichen Vorstellungsvermögens. Trigonometrie von Grund auf - zu Aufgabe 13. Verstehen statt pauken. Visuelle Erklärung komplexer Konzepte. Algebra. Wurzeln, Potenzen und Logarithmen, Funktion und Ableitung. Basis zur Lösung komplexer Probleme des 2. Teils der Prüfung.

Jobtyp: 8
Thema: Prisma

Zustand

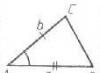
In einem regulären dreieckigen Prisma ABCA_1B_1C_1 sind die Seiten der Basis 4 , und die Seitenkanten 10 . Finden Sie die Schnittfläche des Prismas durch die Ebene, die durch die Mittelpunkte der Kanten AB, AC, A_1B_1 und A_1C_1 verläuft.

Lösung

Betrachten Sie die folgende Abbildung.

Das Segment MN ist Mittellinie Dreieck A_1B_1C_1, also MN = \frac12 B_1C_1=2. Ebenfalls, KL=\frac12BC=2. Außerdem ist MK = NL = 10. Dies impliziert, dass das Viereck MNLK ein Parallelogramm ist. Seit MK\parallel AA_1, dann MK\perp ABC und MK\perp KL. Daher ist das Viereck MNLK ein Rechteck. S_(MNLK) = MK\cdot KL= 10\cdot 2 = 20.

Antworten

Jobtyp: 8
Thema: Prisma

Zustand

Das Volumen der richtigen viereckiges Prisma ABCDA_1B_1C_1D_1 ist 24 . Punkt K ist die Mitte der Kante CC_1. Finden Sie das Volumen der Pyramide KBCD.

Lösung

Gemäß der Bedingung ist KC die Höhe der Pyramide KBCD . CC_1 ist die Höhe des Prismas ABCDA_1B_1C_1D_1 .

Da K der Mittelpunkt von CC_1 ist, dann KC=\frac12CC_1. Dann sei CC_1=H KC=\frac12H. Beachten Sie auch das S_(BCD)=\frac12S_(ABCD). Dann, V_(KBCD)= \frac13S_(BCD)\cdot\frac(H)(2)= \frac13\cdot\frac12S_(ABCD)\cdot\frac(H)(2)= \frac(1)(12)\cdot S_(ABCD)\cdot H= \frac(1)(12)V_(ABCDA_1B_1C_1D_1). Somit, V_(KBCD)=\frac(1)(12)\cdot24=2.

Antworten

Quelle: „Mathematik. Vorbereitung auf die Prüfung-2017. Profilebene. Ed. F. F. Lysenko, S. Yu. Kulabukhova.

Jobtyp: 8
Thema: Prisma

Zustand

Finden Sie die seitliche Oberfläche eines regelmäßigen sechseckigen Prismas, dessen Basisseite 6 und seine Höhe 8 beträgt.

Lösung

Die Fläche der Seitenfläche des Prismas ergibt sich aus der Formel S-Seite. = P Haupt. · h = 6a\cdot h, wobei P main. und h sind jeweils der Umfang der Basis und die Höhe des Prismas, gleich 8 , und a ist die Seite eines regelmäßigen Sechsecks, gleich 6 . Daher S-Seite. = 6\cdot 6\cdot 8 = 288.

Antworten

Quelle: „Mathematik. Vorbereitung auf die Prüfung-2017. Profilebene. Ed. F. F. Lysenko, S. Yu. Kulabukhova.

Jobtyp: 8
Thema: Prisma

Zustand

In einem Gefäß, das die richtige Form hat dreieckiges Prisma gegossenes Wasser. Der Wasserstand erreicht 40 cm, wie hoch wird der Wasserstand sein, wenn man es in ein anderes Gefäß gleicher Form gießt, dessen Grundfläche doppelt so groß ist wie das erste? Geben Sie Ihre Antwort in Zentimetern an.

Lösung

Sei a die Seite des Bodens des ersten Gefäßes, dann ist 2 a die Seite des Bodens des zweiten Gefäßes. Bedingt ist, dass das Flüssigkeitsvolumen V im ersten und zweiten Gefäß gleich ist. Mit H ist das Niveau bezeichnet, auf das die Flüssigkeit im zweiten Gefäß angestiegen ist. Dann V= \frac12\cdot a^2\cdot\sin60^(\circ)\cdot40= \frac(a^2\sqrt3)(4)\cdot40, Und, V=\frac((2a)^2\sqrt3)(4)\cdot H. Von hier \frac(a^2\sqrt3)(4)\cdot40=\frac((2a)^2\sqrt3)(4)\cdot H, 40=4H, H=10.

Antworten

Quelle: „Mathematik. Vorbereitung auf die Prüfung-2017. Profilebene. Ed. F. F. Lysenko, S. Yu. Kulabukhova.

Jobtyp: 8
Thema: Prisma

Zustand

In einem regulären sechseckigen Prisma ABCDEFA_1B_1C_1D_1E_1F_1 sind alle Kanten 2 . Finde den Abstand zwischen den Punkten A und E_1 .

Lösung

Das Dreieck AEE_1 ist rechtwinklig, da die Kante EE_1 senkrecht zur Ebene der Basis des Prismas ist, wird der Winkel AEE_1 ein rechter Winkel sein.

Dann gilt nach dem Satz des Pythagoras AE_1^2 = AE^2 + EE_1^2. Finden Sie AE aus dem Dreieck AFE unter Verwendung des Kosinussatzes. Jeder Innenwinkel eines regelmäßigen Sechsecks ist 120^(\circ). Dann AE^2= AF^2+FE^2-2\cdot AF\cdot FE\cdot\cos120^(\circ)= 2^2+2^2-2\cdot2\cdot2\cdot\links (-\frac12 \rechts).

Daher ist AE^2=4+4+4=12,

AE_1^2=12+4=16,

AE_1=4.

Antworten

Quelle: „Mathematik. Vorbereitung auf die Prüfung-2017. Profilebene. Ed. F. F. Lysenko, S. Yu. Kulabukhova.

Jobtyp: 8
Thema: Prisma

Zustand

Finden Sie die Fläche der Seitenfläche eines geraden Prismas, dessen Basis eine Raute mit Diagonalen gleich ist 4\sqrt5 und 8 und eine Seitenkante gleich 5 .

Lösung

Die Fläche der Seitenfläche eines geraden Prismas ergibt sich aus der Formel S-Seite. = P Haupt. · h = 4a\cdot h, wobei P main. und h, jeweils der Umfang der Basis und die Höhe des Prismas, gleich 5, und a ist die Seite der Raute. Lassen Sie uns die Seite der Raute finden, indem wir die Tatsache nutzen, dass die Diagonalen der Raute ABCD senkrecht aufeinander stehen und der Schnittpunkt in zwei Hälften geteilt ist.

Wir zeichnen separat die Basis des Prismas, d.h. das Dreieck ABC (Abb. 307, a), und vervollständigen es zu einem Rechteck, für das wir eine gerade Linie KM durch die Ecke B || ziehen AC und von den Punkten A und C lassen wir die Senkrechten AF und CE auf diese Linie fallen. Wir erhalten das ACEF-Rechteck. Nachdem wir die Höhe BD des Dreiecks ABC gezeichnet haben, sehen wir, dass das ACEF-Rechteck in 4 rechtwinklige Dreiecke unterteilt ist. Außerdem ist \(\Delta\)ALL = \(\Delta\)BCD und \(\Delta\)BAF = \(\Delta\)BAD. Das bedeutet, dass die Fläche des Rechtecks ​​ACEF doppelt so groß ist wie die Fläche des Dreiecks ABC, also gleich 2S.

Zu diesem Prisma mit der Basis ABC fügen wir Prismen mit den Basen ALL und BAF und der Höhe hinzu H(Abb. 307, b). Wir erhalten ein rechteckiges Parallelepiped mit ACEF-Basis.

Wenn wir dieses Parallelepiped durch eine Ebene schneiden, die durch die Linien BD und BB' verläuft, sehen wir, dass das rechteckige Parallelepiped aus 4 Prismen mit den Basen BCD, ALL, BAD und BAF besteht.

Prismen mit den Basen BCD und ALL können kombiniert werden, da ihre Basen gleich sind (\(\Delta\)BCD = \(\Delta\)BCE) und auch ihre Seitenkanten, die senkrecht auf einer Ebene stehen, gleich sind. Daher sind die Volumina dieser Prismen gleich. Die Volumina von Prismen mit den Basen BAD und BAF sind ebenfalls gleich.

Es stellt sich also heraus, dass das Volumen eines gegebenen dreieckigen Prismas mit der Basis ABC das halbe Volumen ist Quader mit ACEF-Basis.

Wir wissen, dass das Volumen eines rechteckigen Parallelepipeds gleich dem Produkt aus der Fläche seiner Basis und der Höhe ist, d.h. in diesem Fall ist es gleich 2S H. Daher ist das Volumen dieses rechtwinkligen Dreiecksprismas gleich S H.

Das Volumen eines geraden dreieckigen Prismas ist gleich dem Produkt aus der Fläche seiner Basis und der Höhe.

2. Das Volumen eines geraden polygonalen Prismas.

Wenn wir die Grundflächen dreieckiger Prismen durch S 1, S 2 und S 3 und das Volumen dieses polygonalen Prismas durch V bezeichnen, erhalten wir:

V = S1 H+S2 H+ S3 H, oder

V = (S1 + S2 + S3) H.

Und schließlich: V = S H.

Auf die gleiche Weise wird die Formel für das Volumen eines geraden Prismas mit einem beliebigen Polygon an seiner Basis hergeleitet.

Bedeutet, Das Volumen eines geraden Prismas ist gleich dem Produkt aus der Fläche seiner Basis und der Höhe.

Prisma-Volumen

Satz. Das Volumen eines Prismas ist gleich der Grundfläche mal der Höhe.

Wir beweisen diesen Satz zuerst für ein dreieckiges Prisma und dann für ein polygonales.

1) Zeichnen Sie (Abb. 95) durch die Kante AA 1 des dreieckigen Prismas ABCA 1 B 1 C 1 eine Ebene parallel zur Fläche BB 1 C 1 C und durch die Kante CC 1 - eine Ebene parallel zur Fläche AA 1 B1B; dann setzen wir die Ebenen beider Basen des Prismas fort, bis sie sich mit den gezeichneten Ebenen schneiden.

Dann erhalten wir ein Parallelepiped BD 1, das durch die Diagonalebene AA 1 C 1 C in zwei dreieckige Prismen geteilt wird (eines davon ist gegeben). Lassen Sie uns beweisen, dass diese Prismen gleich sind. Dazu zeichnen wir einen senkrechten Schnitt A B C D. Im Abschnitt erhalten Sie ein Parallelogramm, das eine Diagonale ist As In zwei geteilt gleiches Dreieck. Dieses Prisma ist gleich einem solchen geraden Prisma, dessen Basis \(\Delta\) ist ABC, und die Höhe ist die Kante AA 1 . Ein anderes dreieckiges Prisma hat die gleiche Fläche wie eine Linie, deren Basis \(\Delta\) ist adc, und die Höhe ist die Kante AA 1 . Aber zwei gerade Prismen mit gleichen Basen und gleichen Höhen sind gleich (weil sie beim Einbetten kombiniert werden), was bedeutet, dass die Prismen ABCA 1 B 1 C 1 und ADCA 1 D 1 C 1 gleich sind. Daraus folgt, dass das Volumen dieses Prismas halb so groß ist wie das Volumen des Parallelepipeds BD 1 ; Wenn wir also die Höhe des Prismas durch H bezeichnen, erhalten wir:

$$ V_(\Delta ex) = \frac(S_(ABCD)\cdot H)(2) = \frac(S_(ABCD))(2)\cdot H = S_(ABC)\cdot H $$

2) Ziehen Sie durch die Kante AA 1 des Polygonprismas (Abb. 96) die Diagonalebenen AA 1 C 1 C und AA 1 D 1 D.

Dann wird dieses Prisma in mehrere dreieckige Prismen geschnitten. Die Summe der Volumina dieser Prismen ist das gewünschte Volumen. Wenn wir die Bereiche ihrer Basen mit bezeichnen B 1 , B 2 , B 3 und der Gesamthöhe durch H erhalten wir:

Volumen eines polygonalen Prismas = B 1H+ B 2H+ B 3H =( B 1 + B 2 + B 3) H =

= (Fläche ABCDE) H.

Folge. Wenn V, B und H Zahlen sind, die Volumen, Grundfläche und Höhe des Prismas in den entsprechenden Einheiten ausdrücken, dann können wir nach dem Bewiesenen schreiben:

Schüler, die sich auf die Prüfung in Mathematik vorbereiten, sollten unbedingt lernen, wie man Probleme löst, um die Fläche einer geraden Linie zu finden und rechtes Prisma. Die langjährige Praxis bestätigt, dass viele Studenten solche Aufgaben in der Geometrie als ziemlich schwierig empfinden.

Gleichzeitig sollten Gymnasiasten mit jedem Ausbildungsniveau in der Lage sein, die Fläche und das Volumen eines regelmäßigen und direkten Prismas zu finden. Nur in diesem Fall können sie aufgrund der Ergebnisse der bestandenen Prüfung mit Wettbewerbspunkten rechnen.

Wichtige Punkte, an die Sie sich erinnern sollten

• Wenn die Seitenkanten des Prismas senkrecht zur Basis stehen, wird es als gerade bezeichnet. Alle Seitenflächen dieser Figur sind Rechtecke. Die Höhe eines geraden Prismas fällt mit seiner Kante zusammen.
• Ein regelmäßiges Prisma ist eines, dessen Seitenkanten senkrecht zu der Basis sind, die das regelmäßige Vieleck enthält. Die Seitenflächen dieser Figur sind gleiche Rechtecke. Das richtige Prisma ist immer gerade.

Die Vorbereitung auf das Einheitliche Staatsexamen zusammen mit Shkolkovo ist der Schlüssel zu Ihrem Erfolg!

Um den Unterricht so einfach und effektiv wie möglich zu gestalten, wählen Sie unser mathematisches Portal. Hier wird das Ganze präsentiert notwendiges Material um Sie bei der Vorbereitung auf die Zertifizierungsprüfung zu unterstützen.

Spezialisten des Bildungsprojekts "Shkolkovo" schlagen vor, von einfach zu komplex zu gehen: Zuerst geben wir die Theorie, grundlegende Formeln, Theoreme und elementare Probleme mit Lösungen und gehen dann schrittweise zu Aufgaben über Expertenniveau.

Grundlegende Informationen werden im Abschnitt "Theoretische Referenz" systematisiert und übersichtlich dargestellt. Wenn Sie das notwendige Material bereits wiederholt haben, empfehlen wir Ihnen, das Lösen von Aufgaben zum Ermitteln der Fläche und des Volumens eines geraden Prismas zu üben. In der Rubrik "Katalog" wird vorgestellt große AuswahlÜbungen unterschiedliche Grade Schwierigkeiten.

Versuchen Sie jetzt, die Fläche eines geraden und regelmäßigen Prismas zu berechnen. Zerlegen Sie jede Aufgabe. Wenn es keine Schwierigkeiten verursacht hat, können Sie sicher mit Übungen auf Expertenebene fortfahren. Und wenn dennoch gewisse Schwierigkeiten auftreten, empfehlen wir Ihnen, sich zusammen mit dem mathematischen Portal Shkolkovo regelmäßig online auf die Prüfung vorzubereiten, und Aufgaben zum Thema „Direktes und reguläres Prisma“ werden Ihnen leicht fallen.

Im Schullehrplan für den Studiengang Festkörpergeometrie beginnt das Studium dreidimensionaler Figuren meist mit einem einfachen geometrischen Körper - einem Prismenpolyeder. Die Rolle seiner Basen übernehmen 2 gleiche Polygone, die darin liegen parallele Ebenen. Ein Sonderfall ist ein regelmäßiges viereckiges Prisma. Seine Grundflächen sind 2 identische regelmäßige Vierecke, zu denen die Seiten senkrecht stehen und die Form von Parallelogrammen (oder Rechtecken, wenn das Prisma nicht geneigt ist) haben.

Wie sieht ein prisma aus

Ein regelmäßiges viereckiges Prisma ist ein Sechseck, an dessen Basis sich 2 Quadrate befinden und dessen Seitenflächen durch Rechtecke dargestellt werden. Ein anderer Name für diese geometrische Figur ist ein gerades Parallelepiped.

Die Abbildung, die ein viereckiges Prisma darstellt, ist unten gezeigt.

Kann man auch auf dem Bild sehen die wichtigsten Elemente, aus denen ein geometrischer Körper besteht. Sie werden allgemein bezeichnet als:

Manchmal findet man in Geometrieaufgaben das Konzept eines Abschnitts. Die Definition wird so lauten: Ein Schnitt sind alle Punkte eines Volumenkörpers, die zur Schnittebene gehören. Der Schnitt ist senkrecht (schneidet die Kanten der Figur in einem Winkel von 90 Grad). Bei einem rechteckigen Prisma wird auch ein Diagonalschnitt berücksichtigt (es können maximal 2 Schnitte gebaut werden), der durch 2 Kanten und die Diagonalen der Basis verläuft.

Wird der Schnitt so gezeichnet, dass die Schnittebene weder zu den Grund- noch zu den Seitenflächen parallel ist, entsteht ein Prismenstumpf.

Verschiedene Verhältnisse und Formeln werden verwendet, um die reduzierten prismatischen Elemente zu finden. Einige von ihnen sind aus dem Verlauf der Planimetrie bekannt (um beispielsweise die Fläche der Basis eines Prismas zu ermitteln, reicht es aus, sich an die Formel für die Fläche eines Quadrats zu erinnern).

Oberfläche und Volumen

Um das Volumen eines Prismas mithilfe der Formel zu bestimmen, müssen Sie die Fläche seiner Basis und Höhe kennen:

V = Sprim h

Da die Basis eines regulären tetraedrischen Prismas ein Quadrat mit einer Seite ist A, Sie können die Formel in einer detaillierteren Form schreiben:

V = a² h

Wenn wir über einen Würfel sprechen - ein normales Prisma mit Gleiche Länge, Breite und Höhe errechnet sich das Volumen wie folgt:

Um zu verstehen, wie man die seitliche Oberfläche eines Prismas findet, muss man sich seinen Schwung vorstellen.

Aus der Zeichnung ist ersichtlich, dass die Seitenfläche aus 4 gleichen Rechtecken besteht. Seine Fläche errechnet sich aus dem Produkt des Umfangs der Basis und der Höhe der Figur:

Seite = Pos h

Da der Umfang ein Quadrat ist P = 4a, die Formel hat die Form:

Seite = 4a h

Für Würfel:

Seite = 4a²

Um die Gesamtfläche eines Prismas zu berechnen, fügen Sie der Seitenfläche 2 Grundflächen hinzu:

Svoll = SSeite + 2SBasis

Angewendet auf ein viereckiges regelmäßiges Prisma hat die Formel die Form:

Svoll = 4a h + 2a²

Für die Oberfläche eines Würfels:

Svoll = 6a²

Mit Kenntnis des Volumens oder der Oberfläche können Sie die einzelnen Elemente eines geometrischen Körpers berechnen.

Prismenelemente finden

Oft gibt es Probleme, bei denen das Volumen angegeben ist oder der Wert der Seitenfläche bekannt ist, wo es notwendig ist, die Länge der Seite der Basis oder die Höhe zu bestimmen. In solchen Fällen können Formeln abgeleitet werden:

• Grundseitenlänge: a = Seite / 4h = √(V / h);
• Höhe bzw. Seitenrippenlänge: h = Seite / 4a = V / a²;
• Grundfläche: Sprim = V/h;
• Seitenfläche: Seite gr = Seite / 4.

Um zu bestimmen, wie viel Fläche eine Diagonale hat, müssen Sie die Länge der Diagonale und die Höhe der Figur kennen. Für ein Quadrat d = a√2. Deshalb:

Sdiag = ah√2

Um die Diagonale des Prismas zu berechnen, wird die Formel verwendet:

dPreis = √(2a² + h²)

Um zu verstehen, wie die obigen Verhältnisse anzuwenden sind, können Sie einige einfache Aufgaben üben und lösen.

Beispiele für Probleme mit Lösungen

Hier sind einige der Aufgaben, die in den staatlichen Abschlussprüfungen in Mathematik vorkommen.

Übung 1.

Sand wird in eine Kiste gegossen, die wie ein regelmäßiges viereckiges Prisma geformt ist. Die Höhe des Sandes beträgt 10 cm. Wie hoch wird der Sand sein, wenn Sie ihn in einen Behälter mit der gleichen Form, aber mit einer doppelt so langen Basislänge bringen?

Es soll wie folgt argumentiert werden. Die Sandmenge im ersten und zweiten Behälter änderte sich nicht, d. h. sein Volumen darin ist gleich. Sie können die Länge der Basis definieren als A. In diesem Fall beträgt das Volumen des Stoffes für das erste Kästchen:

V₁ = ha² = 10a²

Für die zweite Box ist die Länge der Basis 2a, aber die Höhe des Sandspiegels ist unbekannt:

V₂ = h(2a)² = 4ha²

Weil das V₁ = V₂, können die Ausdrücke gleichgesetzt werden:

10a² = 4ha²

Nachdem wir beide Seiten der Gleichung um a² reduziert haben, erhalten wir:

Als Ergebnis wird die neue Sandebene sein h = 10 / 4 = 2,5 cm.

Aufgabe 2.

ABCDA₁B₁C₁D₁ ist ein regelmäßiges Prisma. Es ist bekannt, dass BD = AB₁ = 6√2. Finden Sie die Gesamtoberfläche des Körpers.

Um besser verständlich zu machen, welche Elemente bekannt sind, können Sie eine Figur zeichnen.

Da es sich um ein regelmäßiges Prisma handelt, können wir daraus schließen, dass die Grundfläche ein Quadrat mit einer Diagonalen von 6√2 ist. Die Diagonale der Seitenfläche hat den gleichen Wert, daher hat die Seitenfläche auch die Form eines Quadrats gleich der Grundfläche. Es stellt sich heraus, dass alle drei Dimensionen – Länge, Breite und Höhe – gleich sind. Wir können daraus schließen, dass ABCDA₁B₁C₁D₁ ein Würfel ist.

Die Länge einer beliebigen Kante wird durch die bekannte Diagonale bestimmt:

a = d / √2 = 6√2 / √2 = 6

Die Gesamtoberfläche ergibt sich aus der Würfelformel:

Svoll = 6a² = 6 6² = 216

Aufgabe 3.

Das Zimmer wird renoviert. Es ist bekannt, dass sein Boden die Form eines Quadrats mit einer Fläche von 9 m² hat. Die Raumhöhe beträgt 2,5 m. Was kostet das Tapezieren eines Raumes am wenigsten, wenn 1 m² 50 Rubel kostet?

Da der Boden und die Decke Quadrate sind, dh regelmäßige Vierecke, und seine Wände senkrecht zu horizontalen Flächen stehen, können wir daraus schließen, dass es sich um ein regelmäßiges Prisma handelt. Es ist notwendig, die Fläche seiner Seitenfläche zu bestimmen.

Die Raumlänge beträgt a = √9 = 3 M.

Der Platz wird tapeziert Seite = 4 3 2,5 = 30 m².

Die niedrigsten Tapetenkosten für diesen Raum betragen 50 30 = 1500 Rubel.

Um Probleme für ein rechteckiges Prisma zu lösen, reicht es also aus, die Fläche und den Umfang eines Quadrats und eines Rechtecks ​​berechnen zu können, sowie die Formeln zur Bestimmung des Volumens und der Oberfläche zu kennen.

So finden Sie die Fläche eines Würfels