الرسم على وجهين وزاوية بينهما. بناء المثلث بثلاثة عناصر

فصل: 7

أهداف الدرس:

• نقل المواد التي يتم دراستها إلى الطلاب قدر الإمكان ؛
• تطوير التفكير والذاكرة والقدرة على استخدام البوصلة بحرية ؛
• محاولة زيادة نشاط واستقلالية الطلاب في إكمال المهام.

معدات:

• بوصلة المدرسة
• منقلة،
• مسطرة،
• بطاقات للدراسة الذاتية.

أثناء الفصول

موضوع الدرس: "مشاكل البناء".

اليوم سوف نتعلم كيفية بناء مثلثات باستخدام ثلاثة عناصر معطاة باستخدام البوصلة والمسطرة.

لبناء مثلث ، يجب أن تكون قادرًا أولاً على بناء جزء مساو لجزء معين ، وزاوية تساوي جزءًا معينًا. بالطبع ، يمكنك القيام بذلك باستخدام مسطرة ذات أقسام ومنقلة ، ولكن في الرياضيات تحتاج أيضًا إلى أن تكون قادرًا على تنفيذ الإنشاءات بمساعدة بوصلة ومسطرة بدون أقسام.

تتضمن أي مهمة بناء أربع مراحل رئيسية:

• تحليل؛
• مبنى؛
• دليل؛
• يذاكر.

تحليل ودراسة المشكلة ضروريان مثل البناء نفسه. من الضروري معرفة الحالات التي يكون فيها للمشكلة حل ، والتي لا يوجد فيها حل.

1. بناء جزء مساو لجزء معين.

2. نبني زاوية تساوي الزاوية المعطاة باستخدام البوصلة والمسطرة.

والآن لننتقل إلى بناء المثلثات وفقًا لثلاثة عناصر.

3. بناء مثلث على ضلعين وزاوية بينهما.

مخطط رقم 3.

منح	مطلوب للبناء	مبنى
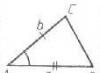
1. أنشئ الزاوية A التي تساوي الزاوية المعطاة. 2. على جانب واحد من الزاوية ، ضع علامة على النقطة C بحيث يكون الجزء AC مساويًا للمقطع المعطى ب. 3. ضع علامة على النقطة B على الجانب الآخر من الزاوية بحيث يكون الجزء AB مساويًا للمقطع المعطى c. 4. قم بتوصيل النقطتين B و C بمسطرة. يتكون المثلث ACB من جانبين وزاوية بينهما.

العمل المستقل للمخطط 3.

الخيار 1.

قم ببناء مثلث BCH إذا كان BC = 3 سم ، CH = 4 سم ، C = 35º.

الخيار 2.

قم ببناء مثلث SDE ، حيث DS = 4 سم ، DE = 5 سم ، D = 110є.

فكرة. قبل إنشاء مثلث ، من الضروري عمل رسم "يدوي" لمثلث ، والذي يوضح جميع العناصر المحددة.

4. بناء مثلث على الضلع والزوايا المجاورة له.

منح	مطلوب للبناء	مبنى
1. ارسم مقطعًا AB بشكل تعسفي يساوي المقطع المعطى c. 2. أنشئ الزاوية A التي تساوي الزاوية المعطاة. 3. أنشئ الزاوية B التي تساوي الزاوية المعطاة. نقطة تقاطع جانبي الزاويتين أ وب هي رأس المثلث ج. أنشئ مثلثًا DAB بمعلومية جانب وزاويتين معطيتين.

العمل المستقل للمخطط 4.

الخيار 1

أنشئ مثلث KMO إذا كان KO = 6 سم ، K = 130º ، O = 20º.

الخيار 2

أنشئ مثلث HRV إذا كانت C = 15º ، D = 50º ، SD = 3 سم.

5. بناء مثلث من ثلاث جهات.

جوهرها هو بناء أي كائن هندسي على أي مجموعة كافية من الشروط الأولية مع وجود بوصلة ومسطرة فقط في متناول اليد. ضع في اعتبارك المخطط العام لأداء مثل هذه المهام:

تحليل المهمة.

يتضمن هذا الجزء إنشاء اتصال بين العناصر التي يجب بناؤها والظروف الأولية للمشكلة. بعد الانتهاء من هذا العنصر ، يجب أن تكون لدينا خطة لحل مشكلتنا.

بناء.

نحن هنا نبني وفقًا للخطة التي وضعناها أعلاه.

دليل.

هنا نثبت أن الشكل الذي أنشأناه يلبي حقًا الشروط الأولية للمشكلة.

يذاكر.

هنا نكتشف البيانات التي بموجبها يكون للمشكلة حل واحد ، يوجد تحته العديد من الحلول ، ولا يوجد حل واحد تحته.

بعد ذلك ، سننظر في مشاكل بناء مثلثات لعناصر ثلاثة مختلفة. هنا لن نأخذ في الاعتبار الإنشاءات الأولية ، مثل مقطع ، زاوية ، إلخ. الآن ، يجب أن تكون لديك بالفعل هذه المهارات.

بناء مثلث بمنح ضلعين وزاوية بينهما

مثال 1

أنشئ مثلثًا إذا كان لدينا جانبان وزاوية بين هذين الضلعين.

تحليل.

دعونا نعطي المقاطع $ AB $ و $ AC $ وزاوية $ α $. نحتاج إلى إنشاء مثلث $ ABC $ بزاوية $ C $ تساوي $ α $.

لنضع خطة بناء:

1. إذا أخذنا $ AB $ كأحد أضلاع الزاوية ، فقد وضعنا جانبًا الزاوية $ BAM $ التي تساوي الزاوية $ α $.
2. في السطر $ AM $ نرسم القطعة $ AC $.
3. ربط النقطتين $ B $ و $ C $.

بناء.

دعونا نبني رسمًا وفقًا للخطة الموضحة أعلاه (الشكل 1).

دليل.

يذاكر.

بما أن مجموع زوايا المثلث يساوي 180 دولارًا ^ \ circ $. هذا يعني أنه إذا كانت الزاوية α أكبر من أو تساوي $ 180 ^ \ circ $ ، فلن يكون هناك حل للمشكلة.

خلاف ذلك ، هناك حل. نظرًا لأن السطر $ a $ خط عشوائي ، فسيكون هناك عدد لا نهائي من هذه المثلثات. ولكن نظرًا لأنهم جميعًا متساوون في العلامة الأولى ، سنفترض أن حل هذه المشكلة فريد من نوعه.

بناء مثلث بثلاثة جوانب

مثال 2

أنشئ مثلثًا إذا كان لدينا ثلاثة أضلاع.

تحليل.

دعونا نعطي المقاطع $ AB $ و $ AC $ و $ BC $. نحتاج لبناء مثلث $ ABC $.

لنضع خطة بناء:

1. ارسم خطًا $ a $ وأنشئ مقطعًا $ AB $ عليه.
2. لننشئ دوائر $ 2 $: الأولى بمركز $ A $ ونصف قطرها $ AC $ ، والثانية بمركز $ B $ ونصف قطرها $ BC $.
3. قم بتوصيل إحدى نقاط تقاطع الدوائر (والتي ستكون النقطة $ C $) بالنقطتين $ A $ و $ B $.

بناء.

دعونا نبني رسمًا وفقًا للخطة الموضحة أعلاه (الشكل 2).

دليل.

يمكن أن نرى من البناء أن جميع الشروط الأولية مستوفاة.

يذاكر.

من متباينة المثلث ، نعلم أن أي ضلع يجب أن يكون أقل من مجموع الضلعين الآخرين. لذلك ، عندما لا يتم استيفاء مثل هذا التفاوت للأجزاء الثلاثة الأصلية ، فلن يكون للمشكلة حل.

نظرًا لأن الدوائر من البناء بها نقطتا تقاطع ، فيمكننا إنشاء مثلثين من هذا القبيل. ولكن نظرًا لأنهم متساوون في المعيار الثالث ، سنفترض أن حل هذه المشكلة فريد من نوعه.

بناء مثلث بمعلومية ضلع وزاويتين متجاورتين

مثال 3

أنشئ مثلثًا إذا كان لدينا جانب واحد وزاويتا $ α $ و $ β $ بجواره.

تحليل.

لنحصل على جزء $ BC $ وزاويتين $ α $ و $ β $. نحتاج إلى إنشاء مثلث $ ABC $ ، حيث $ ∠B = α $ و $ ∠C = β $.

لنضع خطة بناء:

1. ارسم خطًا $ a $ وأنشئ مقطعًا $ BC $ عليه.
2. دعونا نبني الزاوية $ ∠ K = α $ عند الرأس $ B $ إلى الضلع $ BC $.
3. دعونا نبني زاوية $ ∠ M = β $ عند الرأس $ C $ إلى الضلع $ BC $.
4. قم بتوصيل نقطة التقاطع (ستكون هذه النقطة $ A $) للأشعة $ K $ و $ ∠ M $ بالنقطتين $ C $ و $ B $ ،

بناء.

دعونا نبني رسمًا وفقًا للخطة الموضحة أعلاه (الشكل 3).

دليل.

يمكن أن نرى من البناء أن جميع الشروط الأولية مستوفاة.

يذاكر.

بما أن مجموع زوايا المثلث هو 180 دولارًا ^ \ circ $ ، فإن $ α + β≥180 ^ \ circ $ لن يكون لها حل للمشكلة.

خلاف ذلك ، هناك حل. بما أنه يمكننا بناء زوايا من جانبين ، يمكننا بناء مثلثين من هذا القبيل. ولكن نظرًا لأنهم متساوون في المعيار الثاني ، سنفترض أن حل هذه المشكلة فريد من نوعه.

صورة 3 من العرض التقديمي "المثلث 2"لدروس الهندسة حول موضوع "المثلث"

الأبعاد: 720 × 540 بكسل ، التنسيق: jpg. لتنزيل صورة لدرس الهندسة مجانًا ، انقر بزر الماوس الأيمن فوق الصورة وانقر فوق "حفظ الصورة باسم ...". لعرض الصور في الدرس ، يمكنك أيضًا تنزيل العرض التقديمي الكامل "Triangle 2.ppt" مع جميع الصور الموجودة في أرشيف مضغوط مجانًا. حجم الأرشيف - 16 كيلوبايت.

مثلث

"النواقل في الفضاء" - نواقل Codirectional. k (a + b) = ka + kb - قانون التوزيع الأول. أ + ب = ب + أ (قانون الإزاحة). ضرب متجه برقم. المتجه هو قطعة مستقيمة موجهة. النواقل في الفضاء. نواقل Codirectional هي نواقل لها نفس الاتجاه. إذا كانت النواقل ذات اتجاه مشفر وأطوالها متساوية ، فإن هذه المتجهات تسمى متساوية.

"الزاوية بين المتجهات" - إحداثيات المتجهات. متجه الاتجاه مستقيم. التحليل المرئي للمهام من الكتاب المدرسي. إدخال نظام إحداثيات. لنفكر في الخطوط المستقيمة D1B و CB1. كيف يتم العثور على المسافة بين النقاط؟ أوجد الزاوية بين الخطين BD و CD1. الزاوية بين الخطين AB و CD. الزاوية بين النواقل. كيف تجد إحداثيات منتصف الجزء؟

"علماء الرياضيات الكبار" - حصل نظام الإحداثيات الذي اقترحه ديكارت على اسمه. عبر ديكارت عن قانون الحفاظ على الزخم ، وأعطى مفهوم اندفاع القوة. "طريقة" (أو "أفود") و "سباعي منتظم". ليبنيز جوتفريد فيلهلم. كيلديش مستيسلاف فسيفولودوفيتش. إسحاق نيوتن. فيثاغورس من ساموس. حصل جاوس على الدكتوراه عام 1799 من جامعة هيلمستيدت.

"الرياضيات كعلم" - مسابقة "آلة العد". الرياضيات والتاريخ مجالان لا ينفصلان عن المعرفة. جوكوفسكي نيكولاي إيجوروفيتش. ولد سوبوليف في 22 أكتوبر 1793 في مقاطعة نيجني نوفغورود. ليوباتشيفسكي أستاذ في جامعة موسكو و المدرسة التقنية الإمبراطورية. Rebuses. كان والدا ليونارد أويلر Numerator ألكساندروف مدرسين في المدرسة.

"مثلثات متساوية مثلثات" - أي مثلث له ثلاثة وسطاء. مثلث متساوي الأضلاع ومتساوي الساقين. المثلث هو أبسط شكل مسطح. مثلث. ارتفاع المثلث. علامات المساواة بين المثلثات. أدت دراسة المثلث إلى ظهور علم علم المثلثات. أي مثلث له ثلاثة ارتفاعات. عمودي مرسوم من رأس مثلث إلى خط.

"جيب وظيفي" - رسم بياني لغروب الشمس. تاريخ. يتم وصف عملية الغروب بواسطة دالة الجيب المثلثية. متوسط ​​وقت غروب الشمس هو 18 ساعة. باستخدام تقويم مقطوع ، من السهل تحديد لحظة غروب الشمس. هدف. الاستنتاجات. وقت. غروب. علم المثلثات المتنوعة.

المجموع في الموضوع 42 عرضا

نقدم انتباهكم إلى مقطع فيديو تعليمي حول موضوع "إنشاء مثلث بثلاثة عناصر". سوف تكون قادرًا على حل العديد من الأمثلة من فئة مشكلة البناء. سيحلل المعلم بالتفصيل مشكلة بناء المثلث وفقًا لثلاثة عناصر ، ويتذكر أيضًا نظرية المساواة بين المثلثات.

هذا الموضوع له تطبيق عملي واسع ، لذلك سننظر في بعض أنواع حل المشكلات. تذكر أن أي إنشاءات يتم تنفيذها حصريًا بمساعدة البوصلة والمسطرة.

مثال 1:

أنشئ مثلثًا بمنح ضلعين وزاوية بينهما.

معطى: افترض أن المثلث الذي تم تحليله يبدو هكذا

أرز. 1.1 مثلث تم تحليله على سبيل المثال 1

دع المقاطع المعطاة c و a ، والزاوية المعطاة تكون

أرز. 1.2 العناصر المعطاة على سبيل المثال 1

مبنى:

أولا يجب أن تضع جانبا الزاوية 1

أرز. 1.3 الزاوية المتأخرة 1 على سبيل المثال 1

بعد ذلك ، على جانبي زاوية معينة ، نضع جانباً جانبين محددين ببوصلة: نقيس طول الضلع بالبوصلة أونضع رأس البوصلة على قمة الزاوية 1 ، وبالجزء الآخر نصنع شقًا على جانب الزاوية 1. ونقوم بنفس الإجراء مع الجانب مع

أرز. 1.4 الجوانب المؤجلة أو مععلى سبيل المثال 1

ثم نقوم بتوصيل الشقوق الناتجة ، ونحصل على المثلث المطلوب ABC

أرز. 1.5 مثلث مبني ABC على سبيل المثال 1

هل سيكون هذا المثلث مساويا للمثلث المتوقع؟ سيكون ذلك ، لأن عناصر المثلث الناتج (جانبان والزاوية بينهما) متساوية على التوالي مع الجانبين والزاوية بينهما في الحالة. لذلك ، وفقًا للخاصية الأولى للمساواة بين المثلثات - - المثلثات المطلوبة.

اكتمل البناء.

ملحوظة:

تذكر كيف تضع جانبًا زاوية تساوي زاوية معينة.

مثال 2

ضع جانبًا من الشعاع المعطى زاوية تساوي الزاوية المعطاة. أعطيت الزاوية A والشعاع OM. يبني .

مبنى:

أرز. 2.1. الشرط على سبيل المثال 2

1. قم ببناء دائرة Okr (A، r = AB). النقطتان B و C - هما نقطتا التقاطع مع جانبي الزاوية A.

أرز. 2.2. الحل على سبيل المثال 2

1. قم ببناء دائرة Okr (D ، r = CB). النقطتان E و M - هما نقطتا التقاطع مع جانبي الزاوية A.

أرز. 2.3 الحل على سبيل المثال 2

1. زاوية MO هو المطلوب ، منذ ذلك الحين .

اكتمل البناء.

مثال 3

أنشئ مثلثًا ABC بمعلومية ضلع معطى وزاويتين متجاورتين.

دع المثلث الذي تم تحليله يبدو كما يلي:

أرز. 3.1. الشرط على سبيل المثال 3

ثم تبدو الأجزاء المعطاة هكذا

أرز. 3.2 الشرط على سبيل المثال 3

مبنى:

ضع جانبا الزاوية على المستوى

أرز. 3.3 الحل للمثال 3

على جانب الزاوية المعطاة ، دعونا نرسم طول الضلع أ

أرز. 3.4. الحل للمثال 3

ثم قمنا بتأجيل الزاوية من الرأس C. تتقاطع جوانب الزاويتين غير الشائعة γ و α عند النقطة A

أرز. 3.5 الحل للمثال 3

هل المثلث المبني هو المطلوب؟ هو ، نظرًا لأن ضلع المثلث المُنشأ وزاويتين متجاورتين له تساويان على التوالي الضلع والزاوية بينهما ، في الحالة

مطلوب بالمعيار الثاني لتساوي المثلثات

تم البناء

مثال 4

اصنع مثلثًا على ساقين

دع المثلث الذي تم تحليله يبدو هكذا

أرز. 4.1 الشرط على سبيل المثال 4

العناصر المعروفة - الأرجل

أرز. 4.2 الشرط على سبيل المثال 4

تختلف هذه المهمة عن المهام السابقة في أنه يمكن تحديد الزاوية بين الجانبين افتراضيًا - 90 0

مبنى:

ضع جانباً زاوية تساوي 90 0. سنفعل ذلك بنفس الطريقة تمامًا كما هو موضح في المثال 2.

أرز. 4.3 الحل للمثال 4

ثم على جانبي هذه الزاوية ، نضع أطوال الأضلاع جانبًا أو ب، بشرط

أرز. 4.4 الحل للمثال 4

نتيجة لذلك ، يكون المثلث الناتج هو المطلوب ، لأن ضلعيه والزاوية بينهما متساويان على التوالي مع الضلعين والزاوية بينهما ، وفقًا للحالة

لاحظ أنه يمكنك تأجيل الزاوية 90 0 عن طريق إنشاء خطين متعامدين. كيفية أداء هذه المهمة ، ضع في اعتبارك في مثال إضافي

مثال إضافي

استعادة العمود العمودي على الخط p الذي يمر بالنقطة A ،

السطر p ، والنقطة A تقع على هذا الخط

أرز. 5.1 شرط لمثال إضافي

مبنى:

أولاً ، لنقم ببناء دائرة نصف قطرها عشوائي تتمركز عند النقطة أ

أرز. 5.2 الحل لمثال إضافي

هذه الدائرة تتقاطع مع الخط صعند النقطتين K و E. ثم نقوم ببناء دائرتين Okr (K، R = KE)، Okr (E، R = KE). تتقاطع هذه الدوائر عند النقطتين C و B. الجزء SV هو الجزء المطلوب ،

أرز. 5.3 الإجابة على مثال إضافي

1. مجموعة واحدة من الموارد التعليمية الرقمية ().
2. مدرس الرياضيات ().

1. No. 285، 288. Atanasyan L. S.، Butuzov V. F.، Kadomtsev S. B.، Poznyak E. G.، Yudina I. I. تحرير Tikhonov A.N. م: التنوير. 2010
2. أنشئ مثلثًا متساوي الساقين على الجانب والزاوية المقابلة للقاعدة.
3. أنشئ مثلثًا قائمًا بمعلومية الوتر والزاوية الحادة
4. أنشئ مثلثًا بمعرفة الزاوية والارتفاع والمنصف المرسوم من رأس الزاوية المعطاة.