Produkt aus Zahlen mit unterschiedlichen Vorzeichen. Rationale Zahlen multiplizieren und dividieren

Lehrreich:

Förderung von Aktivitäten;

Unterrichtsart

Ausrüstung:

Projektor und Computer.

Unterrichtsplan

1.Organisatorischer Moment

2. Wissen aktualisieren

3. Mathematische Diktate

4.Testausführung

5. Lösung der Übungen

6. Zusammenfassung der Lektion

7. Hausaufgaben.

Während des Unterrichts

1. Organisatorischer Moment

Heute werden wir weiter an der Multiplikation und Division positiver und negativer Zahlen arbeiten. Die Aufgabe eines jeden von Ihnen besteht darin, herauszufinden, wie er dieses Thema beherrscht, und gegebenenfalls zu verfeinern, was noch nicht ganz funktioniert. Darüber hinaus erfahren Sie viel Interessantes über den ersten Frühlingsmonat März. (Folie1)

2. Wissen aktualisieren.

3x=27; -5 x=-45; x:(2,5)=5.

3. Mathematische Diktate(Folie 6.7)

Variante 1

Option 2

4. Testdurchführung ( Folie 8)

Antwort : Martius

5. Lösung der Übungen

(Folien 10 bis 19)

4. März -

2) y×(-2,5)=-15

6 März

3) -50, 4:x=-4, 2

4) -0,25:5×(-260)

13. März

5) -29,12: (-2,08)

14. März

6) (-6-3,6×2,5) ×(-1)

7) -81,6:48×(-10)

17. März

8) 7,15×(-4): (-1,3)

22. März

9) -12,5×50: (-25)

10) 100+(-2,1:0,03)

30. März

6. Zusammenfassung der Lektion

7. Hausaufgaben:

Dokumentinhalte anzeigen
„Zahlen mit unterschiedlichen Vorzeichen multiplizieren und dividieren“

Unterrichtsthema: „Zahlen multiplizieren und dividieren mit.“ verschiedene Zeichen”.

Lernziele: Wiederholung des gelernten Materials zum Thema „Multiplikation und Division von Zahlen mit unterschiedlichen Vorzeichen“, Einübung der Fähigkeiten im Umgang mit den Operationen der Multiplikation und Division einer positiven Zahl durch eine negative Zahl und umgekehrt, sowie eine negative Zahl durch eine negative Zahl.

Lernziele:

Lehrreich:

Konsolidierung der Regeln zu diesem Thema;

Ausbildung von Fähigkeiten und Fertigkeiten zum Umgang mit Operationen der Multiplikation und Division von Zahlen mit unterschiedlichen Vorzeichen.

Lehrreich:

Entwicklung des kognitiven Interesses;

Entwicklung logisches Denken, Gedächtnis, Aufmerksamkeit;

Lehrreich:

Förderung von Aktivitäten;

Den Schülern Fähigkeiten vermitteln unabhängige Arbeit;

Die Liebe zur Natur fördern, das Interesse an Volkszeichen wecken.

Unterrichtsart. Lektionswiederholung und Verallgemeinerung.

Ausrüstung:

Projektor und Computer.

Unterrichtsplan

1.Organisatorischer Moment

2. Wissen aktualisieren

3. Mathematische Diktate

4.Testausführung

5. Lösung der Übungen

6. Zusammenfassung der Lektion

7. Hausaufgaben.

Während des Unterrichts

1. Organisatorischer Moment

Hallo Leute! Was haben wir in den vorherigen Lektionen gemacht? (Multiplizieren und dividieren Rationale Zahlen.)

2. Wissen aktualisieren.

Sehen Sie sich die Regeln zum Multiplizieren und Dividieren positiver und negativer Zahlen an.

Denken Sie an die mnemonische Regel. (Folie 2)

Multiplikation durchführen: (Folie 3)

5x3; 9×(-4); -10×(-8); 36×(-0,1); -20×0,5; -13×(-0,2).

2. Division durchführen: (Folie 4)

48:(-8); -24: (-2); -200:4; -4,9:7; -8,4: (-7); 15:(- 0,3).

3. Lösen Sie die Gleichung: (Folie 5)

3x=27; -5 x=-45; x:(2,5)=5.

3. Mathematische Diktate(Folie 6.7)

Variante 1

Option 2

Die Schüler tauschen Notizbücher aus, schließen den Test ab und geben eine Note ab.

4. Testdurchführung ( Folie 8)

Es war einmal eine Zeit in Russland, in der die Jahre vom 1. März an, vom Beginn des landwirtschaftlichen Frühlings, vom ersten Frühlingsabfall an gezählt wurden. Der März war der „Starter“ des Jahres. Der Name des Monats „März“ stammt von den Römern. Sie haben diesen Monat nach einem ihrer Götter benannt. Mit einem Test können Sie herausfinden, um welche Art von Gott es sich handelt.

Antwort : Martius

Die Römer nannten einen Monat im Jahr Martius zu Ehren des Kriegsgottes Mars. In Rus wurde dieser Name vereinfacht, indem nur die ersten vier Buchstaben verwendet wurden (Folie 9).

Man sagt: „Der März ist untreu, manchmal weint er, manchmal lacht er.“ Es gibt viele Volkszeichen, die mit dem März verbunden sind. Einige seiner Tage haben ihre eigenen Namen. Lassen Sie uns nun alle gemeinsam ein Volksmonatsbuch für März zusammenstellen.

5. Lösung der Übungen

Die Schüler lösen an der Tafel Beispiele, deren Antworten die Tage des Monats sind. An der Tafel erscheint ein Beispiel und dann der Tag des Monats mit dem Namen und Volkszeichen.

(Folien 10 bis 19)

4. März - Arkhip. Auf Arkhip sollten Frauen den ganzen Tag in der Küche verbringen. Je mehr Essen sie zubereitet, desto reicher wird das Haus.

2) y×(-2,5)=-15

6 März- Timofey-Frühling. Wenn am Timofey-Tag Schnee liegt, ist die Ernte für den Frühling.

3) -50, 4:x=-4, 2

4) -0,25:5×(-260)

13. März- Wassili, der Tropfenmacher: Tropfen von den Dächern. Vögel nisten und Zugvögel fliegen von warmen Orten.

5) -29,12: (-2,08)

14. März- Evdokia (Avdotya der Efeu) – der Schnee wird durch den Aufguss flacher. Das zweite Treffen im Frühling (das erste zum Treffen). So wie Evdokia ist, so ist auch der Sommer. Evdokia ist rot – und der Frühling ist rot; Schnee auf Evdokia - für die Ernte.

6) (-6-3,6×2,5) ×(-1)

7) -81,6:48×(-10)

17. März- Gerasim, der Turm, brachte die Türme. Saatkrähen landen auf Ackerland, und wenn sie direkt zu ihren Nestern fliegen, wird es einen freundlichen Frühling geben.

8) 7,15×(-4): (-1,3)

22. März- Elstern - Tag ist gleich Nacht. Der Winter geht zu Ende, der Frühling beginnt, die Lerchen kommen. Nach einem alten Brauch werden aus dem Teig Lerchen und Watvögel gebacken.

9) -12,5×50: (-25)

10) 100+(-2,1:0,03)

30. März- Alexey ist warm. Das Wasser kommt aus den Bergen und die Fische kommen aus dem Lager (von der Winterhütte). Wie auch immer die Bäche an diesem Tag aussehen (groß oder klein), so ist auch die Aue (Überschwemmung).

6. Zusammenfassung der Lektion

Leute, hat euch die heutige Lektion gefallen? Was hast du heute Neues gelernt? Was haben wir wiederholt? Ich schlage vor, dass Sie Ihr eigenes Monatsbuch für April vorbereiten. Sie müssen die Zeichen des Aprils finden und Beispiele mit Antworten erstellen, die dem Tag des Monats entsprechen.

7. Hausaufgaben: S. 218 Nr. 1174, 1179(1) (Folie20)

Lernziele:

Lehrreich:

Formulierung von Regeln für die Multiplikation von Zahlen mit gleichen und unterschiedlichen Vorzeichen;
Beherrschung und Verbesserung der Fähigkeiten zur Multiplikation von Zahlen mit unterschiedlichen Vorzeichen.

Lehrreich:

Entwicklung geistiger Operationen: Vergleich, Verallgemeinerung, Analyse, Analogie;
Entwicklung unabhängiger Arbeitsfähigkeiten;
den Horizont der Studierenden erweitern.

Lehrreich:

Förderung einer Aufzeichnungskultur;
Erziehung zu Verantwortung, Aufmerksamkeit;
Interesse am Thema wecken.

Unterrichtsart: neues Material lernen.

Ausrüstung: Computer, Multimedia-Projektor, Karten für das Spiel „Mathematischer Kampf“, Tests, Wissenskarten.

Plakate an den Wänden:

Wissen ist der edelste Besitz. Jeder strebt danach, aber es kommt nicht von alleine.
Al-Biruni
Bei allem möchte ich auf den Punkt kommen...
B. Pasternak

Unterrichtsplan

Organisatorischer Moment (1 Min.).
Einführung Lehrer (3 Min.).
Mündliche Arbeit (10 Min.).
Präsentation des Materials (15 Min.).
Mathematische Kette (5 Min.).
Hausaufgaben (2 Min.).
Test (6 Min.).
Zusammenfassung der Lektion (3 Min.).

Während des Unterrichts

I. Organisatorischer Moment

Bereitschaft der Schüler für den Unterricht.

II. Eröffnungsrede des Lehrers

Leute, wir haben uns heute nicht umsonst mit euch getroffen, sondern für eine fruchtbare Arbeit: den Wissenserwerb.

Seit es das Universum gibt,
Es gibt niemanden, der kein Wissen braucht.
Welche Sprache und welches Alter wir auch wählen,
Der Mensch strebt seit jeher nach Wissen...
Rudaki

Im Unterricht werden wir lernen Neues Material, festigen Sie es, arbeiten Sie selbstständig, bewerten Sie sich selbst und Ihre Kameraden. Jeder hat eine Wissenskarte auf seinem Schreibtisch, in der unsere Lektion in Etappen unterteilt ist. Die Punkte, die Sie verdient haben unterschiedliche Bühnen Sie selbst tragen die Lektion in diese Karte ein. Und am Ende der Lektion werden wir zusammenfassen. Platzieren Sie diese Karten gut sichtbar.

III. Mündliche Arbeit (in Form des Spiels „Mathematischer Kampf“)

Leute, bevor wir anfangen neues Thema, wiederholen wir, was wir zuvor gelernt haben. Jeder hat ein Blatt Papier mit dem Spiel „Mathematical Combat“ auf seinem Schreibtisch. Die vertikalen und horizontalen Spalten enthalten die Zahlen, die hinzugefügt werden müssen. Diese Zahlen sind mit Punkten markiert. Wir werden die Antworten in die Zellen des Feldes schreiben, in denen sich die Punkte befinden.

Drei Minuten bis zum Abschluss. Wir haben mit der Arbeit begonnen.

Nun tauschten wir Arbeiten mit unserem Schreibtischnachbarn aus und überprüften diese untereinander. Wenn Sie der Meinung sind, dass die Antwort falsch ist, streichen Sie sie sorgfältig durch und schreiben Sie die richtige daneben. Lass uns das Prüfen.

Überprüfen wir nun die Antworten mit dem Bildschirm ( Die richtigen Antworten werden auf die Leinwand projiziert.

Für richtig gelöst

5 Aufgaben werden mit 5 Punkten bewertet;
4 Aufgaben – 4 Punkte;
3 Aufgaben – 3 Punkte;
2 Aufgaben – 2 Punkte;
1 Aufgabe – 1 Punkt.

Gut gemacht. Sie legen alles beiseite. Leute, lasst uns die erzielten Punkte für die „Mathematische Schlacht“ in unsere Wissenskarten eintragen ( Anhang 1).

IV. Präsentation des Materials

Öffnen Sie die Arbeitsmappen. Notieren Sie sich die Nummer, tolle Arbeit.

Welche Operationen mit positiven und negativen Zahlen kennen Sie?
Wie addiere ich zwei negative Zahlen?
Wie addiere ich zwei Zahlen mit unterschiedlichen Vorzeichen?
Wie subtrahiere ich Zahlen mit unterschiedlichen Vorzeichen?
Sie verwenden immer das Wort „Modul“. Was ist der Modul einer Zahl? A?

Das heutige Unterrichtsthema bezieht sich auch auf die Operation von Zahlen mit unterschiedlichen Vorzeichen. Aber es war in einem Anagramm versteckt, in dem man Buchstaben vertauschen muss, um ein bekanntes Wort zu erhalten. Versuchen wir es herauszufinden.

ENOZHEUMNI

Wir schreiben das Thema der Lektion auf: „Multiplikation“.

Der Zweck unserer Lektion: sich mit der Multiplikation positiver und negativer Zahlen vertraut zu machen und Regeln für die Multiplikation von Zahlen mit gleichen und unterschiedlichen Vorzeichen zu formulieren.

Alle Aufmerksamkeit gilt der Tafel. Vor Ihnen liegt eine Tabelle mit Aufgaben, bei deren Lösung wir die Regeln für die Multiplikation positiver und negativer Zahlen formulieren.

2*3 = 6°C;
–2*3 = –6°С;
–2*(–3) = 6°С;
2*(–3) = –6°С;

1. Die Lufttemperatur steigt stündlich um 2°C. Jetzt zeigt das Thermometer 0°C ( Anlage 2– Thermometer) (Folie 1 am Computer).

Wie viel hast du erhalten?(6 ° MIT).
Jemand wird die Lösung an die Tafel schreiben, und wir sind alle in Notizbüchern.
Schauen wir auf das Thermometer. Haben wir die richtige Antwort bekommen? (Folie 2 am Computer).

2. Die Lufttemperatur sinkt stündlich um 2°C. Das Thermometer zeigt jetzt 0°C an (Folie 3 am Computer). Welche Lufttemperatur zeigt das Thermometer nach 3 Stunden an?

Wie viel hast du erhalten?(–6 ° MIT).
Die entsprechende Lösung notieren wir an der Tafel und in Notizbüchern. Analogie zu Aufgabe 1.
.(Folie 4 am Computer).

3. Die Lufttemperatur sinkt stündlich um 2°C. Das Thermometer zeigt jetzt 0°C an (Folie 5 am Computer).

Wie viel hast du erhalten?(6 ° MIT).
Die entsprechende Lösung notieren wir an der Tafel und in Notizbüchern. Analogie zu Aufgabe 1 und 2.
Vergleichen wir das Ergebnis mit dem Thermometerwert.(Folie 6 am Computer).

4. Die Lufttemperatur steigt stündlich um 2°C. Das Thermometer zeigt jetzt 0°C an (Folie 7 am Computer). Welche Lufttemperatur zeigte das Thermometer vor 3 Stunden an?

Wie viel hast du erhalten?(–6 ° MIT).
Die entsprechende Lösung notieren wir an der Tafel und in Notizbüchern. Analogie zu den Aufgaben 1-3.
Vergleichen wir das Ergebnis mit dem Thermometerwert.(Folie 8 am Computer).

Schauen Sie sich Ihre Ergebnisse an. Bei der Multiplikation von Zahlen mit gleichen Vorzeichen (Beispiele 1 und 3), mit welchem Vorzeichen haben Sie das Ergebnis erhalten? (positiv).

Bußgeld. Aber in Beispiel 3 sind beide Faktoren negativ und die Antwort ist positiv. Welches mathematische Konzept ermöglicht es Ihnen, von negativen zu positiven Zahlen zu gelangen? (Modul).

Achtungsregel: Um zwei Zahlen mit den gleichen Vorzeichen zu multiplizieren, müssen Sie ihre Absolutwerte multiplizieren und vor dem Ergebnis ein Pluszeichen setzen. (2 Personen wiederholen).

Kehren wir zu Beispiel 3 zurück. Wie groß sind die Module (–2) und (–3)? Lassen Sie uns diese Module multiplizieren. Wie viel hast du erhalten? Mit welchem Zeichen?

Bei der Multiplikation von Zahlen mit unterschiedlichen Vorzeichen (Beispiele 2 und 4), welches Vorzeichen haben Sie als Antwort erhalten? (Negativ).

Formulieren Sie Ihre eigenen Regeln für die Multiplikation von Zahlen mit unterschiedlichen Vorzeichen.

Regel: Wenn Sie Zahlen mit unterschiedlichen Vorzeichen multiplizieren, müssen Sie deren Module multiplizieren und dem Ergebnis ein Minuszeichen voranstellen. (2 Personen wiederholen).

Kehren wir zu den Beispielen Nr. 2 und Nr. 4 zurück. Wie groß sind ihre Faktoren? Lassen Sie uns diese Module multiplizieren. Wie viel hast du erhalten? Welches Zeichen soll als Ergebnis gegeben werden?

Mit diesen beiden Regeln können Sie auch Brüche multiplizieren: dezimal, gemischt, gewöhnlich.

An der Tafel vor Ihnen liegen mehrere Beispiele. Drei entscheiden wir gemeinsam mit mir, den Rest alleine. Achten Sie auf die Aufnahme und Gestaltung.

Gut gemacht. Schlagen wir die Lehrbücher auf und markieren wir die Regeln, die für die nächste Lektion gelernt werden müssen (Seite 190, §7 (Punkt 35)). Wenn Sie diese Regeln kennen, können Sie in Zukunft die Division positiver und negativer Zahlen schnell meistern.

V. Mathematische Kette

Und nun möchte Dunno überprüfen, wie Sie den neuen Stoff gelernt haben und wird Ihnen ein paar Fragen stellen. Wir müssen die Lösung und Antworten in Notizbüchern aufschreiben ( Anhang 3– Mathematische Kette).

Computerpräsentation
Hallo Leute. Ich sehe, dass Sie sehr klug und neugierig sind, deshalb möchte ich Ihnen ein paar Fragen stellen. Seien Sie vorsichtig, insbesondere bei Schildern.
Meine erste Frage lautet: Multiplizieren Sie (–3) mit (–13).
Zweite Frage: Multiplizieren Sie das, was Sie in der ersten Aufgabe erhalten haben, mit (–0,1).
Dritte Frage: Multiplizieren Sie das Ergebnis der zweiten Aufgabe mit (–2).
Vierte Frage: Multiplizieren Sie (-1/3) mit dem Ergebnis der dritten Aufgabe.
Und die letzte, fünfte Frage: Berechnen Sie den Gefrierpunkt von Quecksilber, indem Sie das Ergebnis der vierten Aufgabe mit 15 multiplizieren.
Danke für die Arbeit. Ich wünsche Ihnen Erfolg.

Leute, schauen wir uns an, wie wir die Aufgaben erledigt haben. Alle standen auf.

Wie viel hast du in der ersten Aufgabe bekommen?

Wer eine andere Antwort hat, setzt sich, und wer sich setzt, dem geben wir 0 Punkte für die mathematische Kette auf der Wissenskartei. Der Rest setzt nichts.

Wie viel hast du in der zweiten Aufgabe bekommen?

Wer eine andere Antwort hat, setzt sich hin und trägt 1 Punkt auf seine Wissenskarte für die mathematische Kette ein.

Wie viel hast du in der dritten Aufgabe bekommen?

Wenn Sie eine andere Antwort haben, setzen Sie sich hin und addieren Sie 2 Punkte zu Ihrer Wissenskarte für die mathematische Kette.

Wie viel hast du in der vierten Aufgabe bekommen?

Wenn Sie eine andere Antwort haben, setzen Sie sich hin und addieren Sie 3 Punkte zu Ihrer Wissenskarte für die mathematische Kette.

Wie viel hast du in der fünften Aufgabe bekommen?

Wer eine andere Antwort hat, setzt sich hin und trägt 4 Punkte auf seine Wissenskarte für die mathematische Kette ein. Die restlichen Jungs haben alle 5 Aufgaben richtig gelöst. Setz dich, du gibst dir 5 Punkte für die mathematische Kette auf deiner Wissenskarte.

Was ist der Gefrierpunkt von Quecksilber?(–39 °C).

VI. Hausaufgaben

§7 (Absatz 35, Seite 190), Nr. 1121 – Lehrbuch: Mathematik. 6. Klasse: [N.Ya.Vilenkin und andere]

Kreative Aufgabe: Schreiben Sie eine Aufgabe zur Multiplikation positiver und negativer Zahlen.

VII. Prüfen

Fahren wir mit der nächsten Stufe der Lektion fort: der Durchführung des Tests ( Anhang 4).

Sie müssen die Aufgaben lösen und die Nummer der richtigen Antwort einkreisen. Für die ersten beiden richtig erledigten Aufgaben erhalten Sie 1 Punkt, für die 3. Aufgabe - 2 Punkte, für die 4. Aufgabe - 3 Punkte. Wir haben mit der Arbeit begonnen.

Δ –1 Punkt;
o –2 Punkte;
-3 Punkte.

Tragen wir nun die Nummern der richtigen Antworten in die Tabelle unter dem Test ein. Schauen wir uns die Ergebnisse an. In den leeren Zellen sollte die Nummer 1418 stehen (Ich schreibe an die Tafel). Wer es erhalten hat, trägt 7 Punkte auf die Wissenskarte. Wer einen Fehler gemacht hat, trägt die Punktezahl nur für richtig erledigte Aufgaben auf der Wissenskartei ein.

Der Große Krieg dauerte genau 1418 Tage. vaterländischer Krieg, ein Sieg, den das russische Volk mit einem hohen Preis erkaufte. Und am 9. Mai 2010 feiern wir den 65. Jahrestag des Sieges über Nazi-Deutschland.

VIII. Zusammenfassung der Lektion

Berechnen wir nun die Gesamtpunktzahl, die Sie für die Lektion erreicht haben, und tragen Sie die Ergebnisse in die Wissenskartei der Schüler ein. Dann teilen wir diese Karten aus.

15 – 17 Punkte – Punktzahl „5“;
10 – 14 Punkte – Punktzahl „4“;
weniger als 10 Punkte – Punktzahl „3“.

Heben Sie Ihre Hände, wer „5“, „4“, „3“ erhalten hat.

Welches Thema haben wir heute behandelt?
So multiplizieren Sie Zahlen mit gleichen Vorzeichen; mit unterschiedlichen Vorzeichen?

Unsere Lektion ist also zu Ende. Ich möchte DANKE für Ihre Arbeit in dieser Lektion sagen.

In diesem Artikel werden wir uns damit befassen Zahlen mit unterschiedlichen Vorzeichen multiplizieren. Hier formulieren wir zunächst die Regel zur Multiplikation positiver und negativer Zahlen, begründen sie und betrachten dann die Anwendung dieser Regel beim Lösen von Beispielen.

Seitennavigation.

Regel zum Multiplizieren von Zahlen mit unterschiedlichen Vorzeichen

Die Multiplikation einer positiven Zahl mit einer negativen Zahl sowie einer negativen Zahl mit einer positiven Zahl erfolgt wie folgt: die Regel zum Multiplizieren von Zahlen mit unterschiedlichen Vorzeichen: Um Zahlen mit unterschiedlichen Vorzeichen zu multiplizieren, müssen Sie multiplizieren und vor das resultierende Produkt ein Minuszeichen setzen.

Schreiben wir es auf diese Regel in wörtlicher Form. Für jede positive reelle Zahl a und jede negative reelle Zahl −b gilt die Gleichheit a·(−b)=−(|a|·|b|) , und auch für eine negative Zahl −a und eine positive Zahl b die Gleichheit (−a)·b=−(|a|·|b|) .

Die Regel zum Multiplizieren von Zahlen mit unterschiedlichen Vorzeichen stimmt voll und ganz überein Eigenschaften von Operationen mit reellen Zahlen. Tatsächlich ist es auf ihrer Grundlage leicht zu zeigen, dass es für reelle und positive Zahlen a und b eine Kette von Gleichheiten der Form gibt a·(−b)+a·b=a·((−b)+b)=a·0=0, was beweist, dass a·(−b) und a·b entgegengesetzte Zahlen sind, was die Gleichheit a·(−b)=−(a·b) impliziert. Und daraus folgt die Gültigkeit der jeweiligen Multiplikationsregel.

Es ist zu beachten, dass die angegebene Regel zur Multiplikation von Zahlen mit unterschiedlichen Vorzeichen sowohl für reelle Zahlen als auch für rationale Zahlen und für ganze Zahlen gilt. Dies folgt aus der Tatsache, dass Operationen mit rationalen und ganzen Zahlen dieselben Eigenschaften haben, die im obigen Beweis verwendet wurden.

Es ist klar, dass die Multiplikation von Zahlen mit unterschiedlichen Vorzeichen gemäß der resultierenden Regel auf die Multiplikation positiver Zahlen hinausläuft.

Es bleiben nur noch Beispiele für die Anwendung der zerlegten Multiplikationsregel bei der Multiplikation von Zahlen mit unterschiedlichen Vorzeichen.

Beispiele für die Multiplikation von Zahlen mit unterschiedlichen Vorzeichen

Schauen wir uns mehrere Lösungen an Beispiele für die Multiplikation von Zahlen mit unterschiedlichen Vorzeichen. Lass uns beginnen mit einfacher Fall, um sich auf die Regelschritte statt auf die Rechenkomplexität zu konzentrieren.

Beispiel.

Multiplizieren Sie die negative Zahl −4 mit der positiven Zahl 5.

Lösung.

Gemäß der Regel zum Multiplizieren von Zahlen mit unterschiedlichen Vorzeichen müssen wir zunächst die Absolutwerte der ursprünglichen Faktoren multiplizieren. Der Modul von −4 ist 4 und der Modul von 5 ist 5, und die Multiplikation der natürlichen Zahlen 4 und 5 ergibt 20. Zum Schluss muss noch ein Minuszeichen vor die resultierende Zahl gesetzt werden, wir haben −20. Damit ist die Multiplikation abgeschlossen.

Kurz gesagt kann die Lösung wie folgt geschrieben werden: (−4) 5=−(4 5)=−20.

Antwort:

(−4)·5=−20.

Beim Multiplizieren Bruchzahlen Mit unterschiedlichen Vorzeichen müssen Sie in der Lage sein, gewöhnliche Brüche, Dezimalzahlen und deren Kombinationen mit natürlichen und gemischten Zahlen zu multiplizieren.

Beispiel.

Multiplizieren Sie Zahlen mit unterschiedlichen Vorzeichen 0, (2) und .

Lösung.

Durch Umwandeln eines periodischen Dezimalbruchs in einen gewöhnlichen Bruch und auch durch Umwandeln einer gemischten Zahl in einen unechten Bruch aus dem ursprünglichen Produkt Kommen wir zum Produkt gewöhnliche Brüche mit unterschiedlichen Vorzeichen der Form. Dieses Produkt ist nach der Regel der Multiplikation von Zahlen mit unterschiedlichen Vorzeichen gleich . Jetzt müssen wir nur noch die gewöhnlichen Brüche in Klammern multiplizieren .

In dieser Lektion geht es um die Multiplikation und Division rationaler Zahlen.

Unterrichtsinhalte

Rationale Zahlen multiplizieren

Die Regeln zur Multiplikation ganzer Zahlen gelten auch für rationale Zahlen. Mit anderen Worten: Um rationale Zahlen zu multiplizieren, müssen Sie dazu in der Lage sein

Außerdem müssen Sie die Grundgesetze der Multiplikation kennen, wie zum Beispiel: das kommutative Gesetz der Multiplikation, das assoziative Gesetz der Multiplikation, das distributive Gesetz der Multiplikation und die Multiplikation mit Null.

Beispiel 1. Finden Sie den Wert eines Ausdrucks

Dies ist die Multiplikation rationaler Zahlen mit unterschiedlichen Vorzeichen. Um rationale Zahlen mit unterschiedlichen Vorzeichen zu multiplizieren, müssen Sie ihre Module multiplizieren und vor der resultierenden Antwort ein Minuszeichen setzen.

Um deutlich zu machen, dass es sich um Zahlen mit unterschiedlichen Vorzeichen handelt, setzen wir jede rationale Zahl zusammen mit ihren Vorzeichen in Klammern

Der Modul der Zahl ist gleich, und der Modul der Zahl ist gleich. Nachdem wir die resultierenden Module als positive Brüche multipliziert hatten, erhielten wir die Antwort, aber vor der Antwort setzten wir ein Minus, wie es die Regel von uns verlangte. Um dieses Minus vor der Antwort sicherzustellen, wurde die Multiplikation der Module in Klammern mit vorangestelltem Minus durchgeführt.

Die Kurzlösung sieht so aus:

Beispiel 2. Finden Sie den Wert eines Ausdrucks

Beispiel 3. Finden Sie den Wert eines Ausdrucks

Dies ist die Multiplikation negativer rationaler Zahlen. Um negative rationale Zahlen zu multiplizieren, müssen Sie ihre Module multiplizieren und vor der resultierenden Antwort ein Pluszeichen setzen

Die Lösung für dieses Beispiel kann kurz geschrieben werden:

Beispiel 4. Finden Sie den Wert eines Ausdrucks

Die Lösung für dieses Beispiel kann kurz geschrieben werden:

Beispiel 5. Finden Sie den Wert eines Ausdrucks

Dies ist die Multiplikation rationaler Zahlen mit unterschiedlichen Vorzeichen. Multiplizieren wir die Module dieser Zahlen und setzen wir vor der resultierenden Antwort ein Minus

Die kurze Lösung wird viel einfacher aussehen:

Beispiel 6. Finden Sie den Wert eines Ausdrucks

Lassen Sie uns die gemischte Zahl in einen unechten Bruch umwandeln. Schreiben wir den Rest so um, wie er ist

Wir haben die Multiplikation rationaler Zahlen mit unterschiedlichen Vorzeichen erhalten. Lassen Sie uns die Module dieser Zahlen multiplizieren und vor der resultierenden Antwort ein Minus setzen. Der Eintrag mit Modulen kann übersprungen werden, um den Ausdruck nicht zu überladen

Die Lösung für dieses Beispiel kann kurz geschrieben werden

Beispiel 7. Finden Sie den Wert eines Ausdrucks

Dies ist die Multiplikation rationaler Zahlen mit unterschiedlichen Vorzeichen. Multiplizieren wir die Module dieser Zahlen und setzen wir vor der resultierenden Antwort ein Minus

Zuerst stellte sich heraus, dass die Antwort ein unechter Bruch war, aber wir haben den ganzen Teil darin hervorgehoben. Beachten Sie, dass der ganzzahlige Teil vom Bruchmodul getrennt wurde. Die resultierende gemischte Zahl wurde in Klammern mit vorangestelltem Minuszeichen eingeschlossen. Dies geschieht, um sicherzustellen, dass die Anforderung der Regel erfüllt wird. Und die Regel verlangte, dass der erhaltenen Antwort ein Minus vorangestellt werden muss.

Die Lösung für dieses Beispiel kann kurz geschrieben werden:

Beispiel 8. Finden Sie den Wert eines Ausdrucks

Lassen Sie uns zunächst die resultierende Zahl mit der verbleibenden Zahl 5 multiplizieren. Wir überspringen den Eintrag mit Modulen, um den Ausdruck nicht zu überladen.

Antwort: Ausdruckswert gleich −2.

Beispiel 9. Finden Sie die Bedeutung des Ausdrucks:

Lass uns übersetzen gemischte Zahlen zu unechten Brüchen:

Wir haben die Multiplikation negativer rationaler Zahlen erhalten. Lassen Sie uns die Module dieser Zahlen multiplizieren und vor der resultierenden Antwort ein Pluszeichen setzen. Der Eintrag mit Modulen kann übersprungen werden, um den Ausdruck nicht zu überladen

Beispiel 10. Finden Sie den Wert eines Ausdrucks

Der Ausdruck besteht aus mehreren Faktoren. Wenn ein Ausdruck aus mehreren Faktoren besteht, hängt das Produkt nach dem assoziativen Multiplikationsgesetz nicht von der Reihenfolge der Aktionen ab. Dadurch können wir einen bestimmten Ausdruck in beliebiger Reihenfolge auswerten.

Erfinden wir das Rad nicht neu, sondern berechnen wir diesen Ausdruck von links nach rechts in der Reihenfolge der Faktoren. Lassen Sie uns den Eintrag mit Modulen überspringen, um den Ausdruck nicht zu überladen

Dritte Aktion:

Vierte Aktion:

Antwort: Der Wert des Ausdrucks ist

Beispiel 11. Finden Sie den Wert eines Ausdrucks

Erinnern wir uns an das Gesetz der Multiplikation mit Null. Dieses Gesetz besagt, dass ein Produkt gleich Null ist, wenn mindestens einer der Faktoren gleich Null ist.

In unserem Beispiel ist einer der Faktoren gleich Null, also antworten wir ohne Zeitverlust, dass der Wert des Ausdrucks gleich Null ist:

Beispiel 12. Finden Sie den Wert eines Ausdrucks

Das Produkt ist gleich Null, wenn mindestens einer der Faktoren gleich Null ist.

In unserem Beispiel ist einer der Faktoren gleich Null, also antworten wir ohne Zeitverlust auf den Wert des Ausdrucks gleich Null:

Beispiel 13. Finden Sie den Wert eines Ausdrucks

Sie können die Reihenfolge der Aktionen verwenden und zunächst den Ausdruck in Klammern berechnen und die resultierende Antwort mit einem Bruch multiplizieren.

Sie können auch das Verteilungsgesetz der Multiplikation verwenden – multiplizieren Sie jeden Term der Summe mit einem Bruch und addieren Sie die resultierenden Ergebnisse. Wir werden diese Methode verwenden.

Wenn ein Ausdruck Addition und Multiplikation enthält, muss entsprechend der Reihenfolge der Operationen zuerst die Multiplikation durchgeführt werden. Deshalb setzen wir im resultierenden neuen Ausdruck die Parameter in Klammern, die multipliziert werden müssen. Auf diese Weise können wir klar erkennen, welche Aktionen früher und welche später durchgeführt werden müssen:

Dritte Aktion:

Antwort: Ausdruckswert gleicht

Die Lösung für dieses Beispiel kann viel kürzer geschrieben werden. Es wird so aussehen:

Es ist klar, dass dieses Beispiel sogar im Kopf gelöst werden könnte. Daher sollten Sie die Fähigkeit entwickeln, einen Ausdruck zu analysieren, bevor Sie ihn lösen. Es ist wahrscheinlich, dass es mental gelöst werden kann und viel Zeit und Nerven spart. Und bei Tests und Prüfungen ist Zeit bekanntlich sehr wertvoll.

Beispiel 14. Finden Sie den Wert des Ausdrucks −4,2 × 3,2

Dies ist die Multiplikation rationaler Zahlen mit unterschiedlichen Vorzeichen. Multiplizieren wir die Module dieser Zahlen und setzen wir vor der resultierenden Antwort ein Minus

Beachten Sie, wie die Module rationaler Zahlen multipliziert wurden. In diesem Fall brauchte man zur Multiplikation der Moduli rationaler Zahlen .

Beispiel 15. Finden Sie den Wert des Ausdrucks −0,15 × 4

Dies ist die Multiplikation rationaler Zahlen mit unterschiedlichen Vorzeichen. Multiplizieren wir die Module dieser Zahlen und setzen wir vor der resultierenden Antwort ein Minus

Beachten Sie, wie die Module rationaler Zahlen multipliziert wurden. In diesem Fall war es notwendig, dazu in der Lage zu sein, um die Module rationaler Zahlen zu multiplizieren.

Beispiel 16. Finden Sie den Wert des Ausdrucks −4,2 × (−7,5)

Dies ist die Multiplikation negativer rationaler Zahlen. Lassen Sie uns die Module dieser Zahlen multiplizieren und vor der resultierenden Antwort ein Pluszeichen setzen

Division rationaler Zahlen

Die Regeln zur Division ganzer Zahlen gelten auch für rationale Zahlen. Mit anderen Worten: Um rationale Zahlen dividieren zu können, muss man dazu in der Lage sein

Ansonsten werden die gleichen Methoden zur Division von gewöhnlichen und dezimalen Brüchen verwendet. Um einen gewöhnlichen Bruch durch einen anderen Bruch zu dividieren, müssen Sie den ersten Bruch mit dem Kehrwert des zweiten Bruchs multiplizieren.

Und teilen Dezimal Um einen anderen Dezimalbruch zu konvertieren, müssen Sie den Dezimalpunkt im Dividenden und im Divisor um so viele Stellen nach rechts verschieben, wie hinter dem Dezimalpunkt im Divisor sind, und dann die Division wie bei einer regulären Zahl durchführen.

Beispiel 1. Finden Sie die Bedeutung des Ausdrucks:

Dies ist die Division rationaler Zahlen mit unterschiedlichen Vorzeichen. Um einen solchen Ausdruck zu berechnen, müssen Sie den ersten Bruch mit dem Kehrwert des zweiten multiplizieren.

Also multiplizieren wir den ersten Bruch mit dem Kehrwert des zweiten.

Wir haben die Multiplikation rationaler Zahlen mit unterschiedlichen Vorzeichen erhalten. Und wir wissen bereits, wie man solche Ausdrücke berechnet. Dazu müssen Sie die Moduli dieser rationalen Zahlen multiplizieren und der resultierenden Antwort ein Minus voranstellen.

Lassen Sie uns dieses Beispiel bis zum Ende vervollständigen. Der Eintrag mit Modulen kann übersprungen werden, um den Ausdruck nicht zu überladen

Der Wert des Ausdrucks ist also

Die detaillierte Lösung lautet wie folgt:

Eine kurze Lösung würde so aussehen:

Beispiel 2. Finden Sie den Wert eines Ausdrucks

Dies ist die Division rationaler Zahlen mit unterschiedlichen Vorzeichen. Um diesen Ausdruck zu berechnen, müssen Sie den ersten Bruch mit dem Kehrwert des zweiten multiplizieren.

Der Kehrwert des zweiten Bruchs ist der Bruch. Multiplizieren wir den ersten Bruch damit:

Eine kurze Lösung würde so aussehen:

Beispiel 3. Finden Sie den Wert eines Ausdrucks

Dies ist die Division negativer rationaler Zahlen. Um diesen Ausdruck zu berechnen, müssen Sie erneut den ersten Bruch mit dem Kehrwert des zweiten multiplizieren.

Der Kehrwert des zweiten Bruchs ist der Bruch. Multiplizieren wir den ersten Bruch damit:

Wir haben die Multiplikation negativer rationaler Zahlen erhalten. Wir wissen bereits, wie ein solcher Ausdruck berechnet wird. Sie müssen die Moduli rationaler Zahlen multiplizieren und vor der resultierenden Antwort ein Pluszeichen setzen.

Lassen Sie uns dieses Beispiel bis zum Ende durcharbeiten. Sie können den Eintrag mit Modulen überspringen, um den Ausdruck nicht zu überladen:

Beispiel 4. Finden Sie den Wert eines Ausdrucks

Um diesen Ausdruck zu berechnen, müssen Sie die erste Zahl −3 mit dem Umkehrbruch von multiplizieren.

Der Kehrwert eines Bruchs ist der Bruch. Multiplizieren Sie die erste Zahl −3 damit

Beispiel 6. Finden Sie den Wert eines Ausdrucks

Um diesen Ausdruck zu berechnen, müssen Sie den ersten Bruch mit dem Kehrwert von 4 multiplizieren.

Der Kehrwert der Zahl 4 ist ein Bruch. Multiplizieren Sie den ersten Bruch damit

Beispiel 5. Finden Sie den Wert eines Ausdrucks

Um diesen Ausdruck zu berechnen, müssen Sie den ersten Bruch mit dem Kehrwert von −3 multiplizieren

Der Kehrwert von −3 ist ein Bruch. Multiplizieren wir den ersten Bruch damit:

Beispiel 6. Finden Sie den Wert des Ausdrucks −14,4: 1,8

Dies ist die Division rationaler Zahlen mit unterschiedlichen Vorzeichen. Um diesen Ausdruck zu berechnen, müssen Sie den Modul des Dividenden durch den Modul des Divisors dividieren und vor der resultierenden Antwort ein Minus setzen.

Beachten Sie, wie der Modul des Dividenden durch den Modul des Divisors dividiert wurde. Um es richtig zu machen, musste man in diesem Fall dazu in der Lage sein.

Wenn Sie sich nicht mit Dezimalzahlen herumschlagen wollen (und das passiert oft), dann wandeln Sie diese gemischten Zahlen in unechte Brüche um und führen Sie dann die Division selbst durch.

Berechnen wir auf diese Weise den vorherigen Ausdruck −14,4: 1,8. Lassen Sie uns Dezimalzahlen in gemischte Zahlen umwandeln:

Nun wandeln wir die resultierenden gemischten Zahlen in unechte Brüche um:

Jetzt können Sie direkt dividieren, also einen Bruch durch einen Bruch dividieren. Dazu müssen Sie den ersten Bruch mit dem umgekehrten Bruch des zweiten multiplizieren:

Beispiel 7. Finden Sie den Wert eines Ausdrucks

Wandeln wir den Dezimalbruch −2,06 in einen unechten Bruch um und multiplizieren diesen Bruch mit dem Kehrwert des zweiten Bruchs:

Mehrstöckige Brüche

Sie können oft auf einen Ausdruck stoßen, bei dem die Division von Brüchen mithilfe eines Bruchstrichs geschrieben wird. Der Ausdruck könnte beispielsweise wie folgt geschrieben werden:

Was ist der Unterschied zwischen den Ausdrücken und ? Es gibt wirklich keinen Unterschied. Diese beiden Ausdrücke haben die gleiche Bedeutung und wir können ein Gleichheitszeichen zwischen ihnen setzen:

Im ersten Fall ist das Divisionszeichen ein Doppelpunkt und der Ausdruck wird in eine Zeile geschrieben. Im zweiten Fall wird die Division von Brüchen mithilfe einer Bruchlinie geschrieben. Das Ergebnis ist ein Bruchteil, dem die Leute zustimmen, ihn anzurufen mehrstöckig.

Wenn Sie auf solche mehrstöckigen Ausdrücke stoßen, müssen Sie dieselben Regeln für die Division gewöhnlicher Brüche anwenden. Der erste Bruch muss mit dem Kehrwert des zweiten multipliziert werden.

Es ist äußerst umständlich, solche Brüche in einer Lösung zu verwenden, daher können Sie sie in einer verständlichen Form schreiben, indem Sie einen Doppelpunkt anstelle eines Bruchstrichs als Divisionszeichen verwenden.

Schreiben wir zum Beispiel einen mehrstöckigen Bruchteil in verständlicher Form. Dazu müssen Sie zunächst herausfinden, wo sich der erste Bruch und der zweite befindet, da dies nicht immer richtig möglich ist. Mehrstöckige Brüche haben mehrere Bruchlinien, die verwirrend sein können. Der Hauptbruchstrich, der den ersten Bruch vom zweiten trennt, ist normalerweise länger als der Rest.

Nachdem Sie die Hauptbruchlinie bestimmt haben, können Sie leicht erkennen, wo sich der erste Bruch und wo der zweite befindet:

Beispiel 2.

Wir finden die Hauptbruchlinie (sie ist die längste) und sehen, dass die ganze Zahl −3 durch einen gemeinsamen Bruch geteilt wird

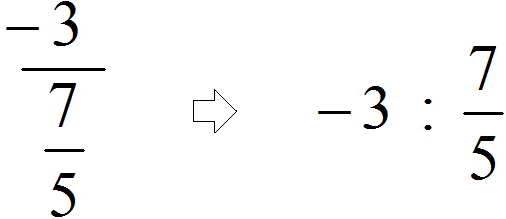
Und wenn wir fälschlicherweise die zweite Bruchlinie als Hauptlinie (die kürzere) nehmen würden, würde sich herausstellen, dass wir den Bruch durch die ganze Zahl 5 dividieren. In diesem Fall würde, selbst wenn dieser Ausdruck korrekt berechnet wird, die Das Problem wird falsch gelöst, da der Dividend in diesem Fall die Zahl −3 ist und der Divisor der Bruch ist.

Beispiel 3. Schreiben wir den mehrstufigen Bruch in verständlicher Form

Wir finden die Hauptbruchlinie (sie ist die längste) und sehen, dass der Bruch durch die ganze Zahl 2 geteilt wird

Und wenn wir fälschlicherweise die erste Bruchlinie als führende Linie (die kürzere) nehmen würden, würde sich herausstellen, dass wir die ganze Zahl −5 durch den Bruch dividieren. In diesem Fall, selbst wenn dieser Ausdruck korrekt berechnet wird, Das Problem wird falsch gelöst, da der Dividend in diesem Fall der Bruch ist und der Divisor die ganze Zahl 2 ist.

Obwohl die Arbeit mit mehrstufigen Brüchen umständlich ist, werden wir ihnen sehr häufig begegnen, insbesondere beim Studium der höheren Mathematik.

Natürlich erfordert es zusätzlichen Zeit- und Platzbedarf, um einen mehrstöckigen Bruchteil in eine verständliche Form zu übersetzen. Daher können Sie mehr verwenden schnelle Methode. Diese Methode ist praktisch und die Ausgabe ermöglicht es Ihnen, einen vorgefertigten Ausdruck zu erhalten, in dem der erste Bruch bereits mit dem Kehrwert des zweiten Bruchs multipliziert wurde.

Diese Methode wird wie folgt implementiert:

Wenn der Bruchteil beispielsweise vierstöckig ist, wird die im ersten Stock liegende Nummer auf den obersten Stock angehoben. Und die Figur im zweiten Stock wird in den dritten Stock gehoben. Die resultierenden Zahlen müssen mit Multiplikationszeichen (×) verbunden werden.

Als Ergebnis erhalten wir unter Umgehung der Zwischennotation einen neuen Ausdruck, in dem der erste Bruch bereits mit dem Kehrwert des zweiten Bruchs multipliziert wurde. Bequemlichkeit und das war's!

Um Fehler bei der Verwendung zu vermeiden diese Methode, können Sie sich an der folgenden Regel orientieren:

Vom ersten bis zum vierten. Vom zweiten zum dritten.

In der Regel wir reden überüber die Böden. Die Figur aus dem ersten Stock muss in den vierten Stock gehoben werden. Und die Figur aus dem zweiten Stock muss in den dritten Stock gehoben werden.

Versuchen wir, mithilfe der obigen Regel einen mehrstöckigen Bruch zu berechnen.

Wir erhöhen also die Nummer im ersten Stock in den vierten Stock und die Nummer im zweiten Stock in den dritten Stock

Als Ergebnis erhalten wir unter Umgehung der Zwischennotation einen neuen Ausdruck, in dem der erste Bruch bereits mit dem Kehrwert des zweiten Bruchs multipliziert wurde. Als nächstes können Sie Ihr vorhandenes Wissen nutzen:

Versuchen wir, einen mehrstufigen Bruch mit einem neuen Schema zu berechnen.

Es gibt nur die erste, zweite und vierte Etage. Es gibt keine dritte Etage. Wir weichen jedoch nicht vom Grundschema ab: Wir erhöhen die Figur vom ersten Stock in den vierten Stock. Und da es keinen dritten Stock gibt, belassen wir die Nummer im zweiten Stock so wie sie ist

Als Ergebnis erhielten wir unter Umgehung der Zwischennotation einen neuen Ausdruck, in dem die erste Zahl −3 bereits mit dem Kehrwert der zweiten Zahl multipliziert wurde. Als nächstes können Sie Ihr vorhandenes Wissen nutzen:

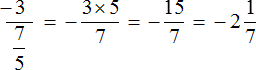
Versuchen wir, den mehrstöckigen Anteil mit dem neuen Schema zu berechnen.

Es gibt nur die zweite, dritte und vierte Etage. Es gibt kein Erdgeschoss. Da es keinen ersten Stock gibt, gibt es keinen Aufstieg in den vierten Stock, aber wir können die Zahl vom zweiten Stock in den dritten erhöhen:

Als Ergebnis erhielten wir unter Umgehung der Zwischennotation einen neuen Ausdruck, bei dem der erste Bruch bereits mit dem Kehrwert des Divisors multipliziert wurde. Als nächstes können Sie Ihr vorhandenes Wissen nutzen:

Verwenden von Variablen

Wenn der Ausdruck komplex ist und Sie den Eindruck haben, dass er Sie bei der Lösung des Problems verwirren wird, können Sie einen Teil des Ausdrucks in eine Variable einfügen und dann mit dieser Variablen arbeiten.

Mathematiker tun dies oft. Ein komplexes Problem wird in einfachere Teilaufgaben zerlegt und gelöst. Anschließend werden die gelösten Teilaufgaben zu einem Ganzen zusammengefasst. Dies ist ein kreativer Prozess, den man im Laufe der Jahre durch hartes Training lernt.

Die Verwendung von Variablen ist bei der Arbeit mit mehrstufigen Brüchen gerechtfertigt. Zum Beispiel:

Finden Sie den Wert eines Ausdrucks

Es gibt also einen Bruchausdruck im Zähler und in dessen Nenner Bruchausdrücke. Mit anderen Worten, wir stehen wieder vor einem mehrstöckigen Bruchteil, der uns nicht so gut gefällt.

Der Ausdruck im Zähler kann in eine Variable mit beliebigem Namen eingegeben werden, zum Beispiel:

In der Mathematik ist es in einem solchen Fall jedoch üblich, Variablen mit lateinischen Großbuchstaben zu benennen. Brechen wir nicht mit dieser Tradition und kennzeichnen Sie den ersten Ausdruck mit einem großen Lateinischer Buchstabe A

Und der Ausdruck im Nenner kann mit dem Großbuchstaben B bezeichnet werden

Jetzt nimmt unser ursprünglicher Ausdruck die Form an. Das heißt, wir haben den numerischen Ausdruck durch einen Buchstaben ersetzt, nachdem wir zuvor den Zähler und den Nenner in die Variablen A und B eingegeben haben.

Jetzt können wir die Werte der Variablen A und den Wert der Variablen B separat berechnen. Die fertigen Werte werden wir in den Ausdruck einfügen.

Lassen Sie uns den Wert der Variablen ermitteln A

Lassen Sie uns den Wert der Variablen ermitteln B

Ersetzen wir nun ihre Werte anstelle der Variablen A und B in den Hauptausdruck:

Wir haben einen mehrstöckigen Bruchteil erhalten, in dem wir das Schema „vom ersten zum vierten, vom zweiten zum dritten“ verwenden können, d Die Nummer befindet sich im zweiten Stock bis zum dritten Stock. Weitere Berechnungen werden nicht schwierig sein:

Somit ist der Wert des Ausdrucks −1.

Natürlich haben wir darüber nachgedacht einfachstes Beispiel, aber unser Ziel war es zu lernen, wie wir Variablen nutzen können, um uns die Arbeit zu erleichtern und Fehler zu minimieren.

Beachten Sie auch, dass die Lösung für dieses Beispiel ohne die Verwendung von Variablen geschrieben werden kann. Es wird so aussehen

Diese Lösung ist schneller und kürzer, und in diesem Fall ist es sinnvoller, sie so zu schreiben. Wenn sich jedoch herausstellt, dass der Ausdruck komplex ist und aus mehreren Parametern, Klammern, Wurzeln und Potenzen besteht, ist es ratsam, ihn zu berechnen mehrere Stufen, wobei ein Teil seiner Ausdrücke in Variablen eingegeben wird.

Hat dir die Lektion gefallen?
Treten Sie unserer neuen VKontakte-Gruppe bei und erhalten Sie Benachrichtigungen über neue Lektionen

Jetzt lasst uns damit umgehen Multiplikation und Division.

Nehmen wir an, wir müssen +3 mit -4 multiplizieren. Wie kann man das machen?

Betrachten wir einen solchen Fall. Drei Personen sind verschuldet und jeder hat 4 $ Schulden. Wie hoch ist die Gesamtverschuldung? Um es zu finden, müssen Sie alle drei Schulden addieren: 4 Dollar + 4 Dollar + 4 Dollar = 12 Dollar. Wir haben entschieden, dass die Addition der drei Zahlen 4 als 3x4 bezeichnet wird. Da es sich in diesem Fall um Schulden handelt, steht vor der 4 ein „-“. Wir wissen, dass die Gesamtverschuldung 12 $ beträgt, daher lautet unser Problem nun 3x(-4)=-12.

Das gleiche Ergebnis erhalten wir, wenn gemäß der Aufgabe jede der vier Personen Schulden in Höhe von 3 $ hat. Mit anderen Worten: (+4)x(-3)=-12. Und da die Reihenfolge der Faktoren keine Rolle spielt, erhalten wir (-4)x(+3)=-12 und (+4)x(-3)=-12.

Fassen wir die Ergebnisse zusammen. Wenn Sie eine positive und eine negative Zahl multiplizieren, ist das Ergebnis immer eine negative Zahl. Der Zahlenwert der Antwort ist derselbe wie bei positiven Zahlen. Produkt (+4)x(+3)=+12. Das Vorhandensein des „-“-Zeichens wirkt sich nur auf das Vorzeichen aus, hat jedoch keinen Einfluss auf den Zahlenwert.

Wie multipliziert man zwei negative Zahlen?

Leider ist es sehr schwierig, zu diesem Thema ein passendes Beispiel aus der Praxis zu finden. Es ist leicht, sich eine Verschuldung von 3 oder 4 Dollar vorzustellen, aber es ist absolut unmöglich, sich -4 oder -3 Menschen vorzustellen, die Schulden gemacht haben.

Vielleicht gehen wir einen anderen Weg. Wenn sich bei der Multiplikation das Vorzeichen eines der Faktoren ändert, ändert sich auch das Vorzeichen des Produkts. Wenn wir die Vorzeichen beider Faktoren ändern, müssen wir uns zweimal ändern Werkmarke, zuerst von positiv nach negativ und dann umgekehrt, von negativ nach positiv, das heißt, das Produkt hat ein Anfangszeichen.

Daher ist es ziemlich logisch, wenn auch etwas seltsam, dass (-3) x (-4) = +12.

Zeichenposition Wenn man es multipliziert, ändert es sich wie folgt:

positive Zahl x positive Zahl = positive Zahl;
negative Zahl x positive Zahl = negative Zahl;
positive Zahl x negative Zahl = negative Zahl;
negative Zahl x negative Zahl = positive Zahl.

Mit anderen Worten, Wenn wir zwei Zahlen mit den gleichen Vorzeichen multiplizieren, erhalten wir eine positive Zahl. Wenn wir zwei Zahlen mit unterschiedlichen Vorzeichen multiplizieren, erhalten wir eine negative Zahl.

Die gleiche Regel gilt für die der Multiplikation entgegengesetzte Aktion – für.

Sie können dies leicht überprüfen, indem Sie ausführen inverse Multiplikationsoperationen. Wenn Sie in jedem der obigen Beispiele den Quotienten mit dem Divisor multiplizieren, erhalten Sie den Dividenden und stellen sicher, dass er das gleiche Vorzeichen hat, zum Beispiel (-3)x(-4)=(+12).

Da der Winter naht, ist es an der Zeit, darüber nachzudenken, welche Schuhe Sie Ihrem eisernen Pferd anziehen, damit Sie auf dem Eis nicht ausrutschen und sich auf winterlichen Straßen sicher fühlen. Sie können beispielsweise Yokohama-Reifen auf der Website mvo.ru oder anderen kaufen. Hauptsache, sie sind von hoher Qualität. Weitere Informationen und Preise finden Sie auf der Website Mvo.ru.