Kuondoa sababu ya kawaida kwenye mabano. Kuweka mabano sababu ya kawaida, sheria, mifano

Katika somo hili tutafahamiana na sheria za kuweka jambo la kawaida nje ya mabano na kujifunza jinsi ya kuipata ndani. mifano mbalimbali na misemo. Hebu tuzungumze kuhusu jinsi operesheni rahisi, kuweka sababu ya kawaida nje ya mabano inakuwezesha kurahisisha mahesabu. Tutaunganisha ujuzi na ujuzi uliopatikana kwa kuangalia mifano ya magumu mbalimbali.

Ni jambo gani la kawaida, kwa nini utafute na kwa madhumuni gani inachukuliwa nje ya mabano? Hebu tujibu maswali haya kwa kuangalia mfano rahisi.

Wacha tusuluhishe equation. Upande wa kushoto equation ni polynomial inayojumuisha maneno sawa. Sehemu ya barua ni ya kawaida kwa maneno haya, ambayo ina maana itakuwa jambo la kawaida. Wacha tuiweke nje ya mabano:

Katika kesi hii, kuchukua kipengele cha kawaida kutoka kwa mabano kulitusaidia kubadilisha polynomial hadi monomial. Kwa hivyo, tuliweza kurahisisha polynomia na mabadiliko yake yalitusaidia kutatua mlingano.

Katika mfano uliozingatiwa, jambo la kawaida lilikuwa dhahiri, lakini ingekuwa rahisi sana kuipata katika polynomial ya kiholela?

Wacha tupate maana ya usemi:.

Katika mfano huu, kuweka sababu ya kawaida nje ya mabano imerahisisha hesabu.

Hebu tutatue mfano mmoja zaidi. Hebu tuthibitishe mgawanyiko katika misemo.

Usemi unaotokana unaweza kugawanywa na , kama inavyohitajika kuthibitishwa. Kwa mara nyingine tena, kuchukua sababu ya kawaida ilituruhusu kutatua tatizo.

Hebu tutatue mfano mmoja zaidi. Wacha tuthibitishe kuwa usemi huo unaweza kugawanywa kwa nambari yoyote asilia: .

Usemi huo ni bidhaa ya nambari mbili za asili zilizo karibu. Mojawapo ya nambari hizi mbili hakika itakuwa sawa, ambayo inamaanisha kuwa usemi utagawanywa na .

Tumeipanga mifano tofauti, lakini walitumia njia sawa ya suluhisho: walichukua sababu ya kawaida kutoka kwa mabano. Tunaona kwamba operesheni hii rahisi hurahisisha sana mahesabu. Ilikuwa rahisi kupata sababu ya kawaida kwa kesi hizi maalum, lakini nini cha kufanya katika kesi ya jumla, kwa polynomial ya kiholela?

Kumbuka kwamba polynomial ni jumla ya monomia.

Fikiria polynomial . Polynomial hii ni jumla ya monomia mbili. Monomia ni bidhaa ya nambari, mgawo, na sehemu ya herufi. Kwa hivyo, katika polynomial yetu, kila monomial inawakilishwa na bidhaa ya nambari na nguvu, bidhaa ya sababu. Sababu zinaweza kuwa sawa kwa monomials zote. Ni mambo haya ambayo yanahitajika kuamua na kuchukuliwa nje ya bracket. Kwanza, tunapata sababu ya kawaida ya coefficients, ambayo ni integer.

Ilikuwa rahisi kupata sababu ya kawaida, lakini hebu tufafanue gcd ya coefficients: .

Hebu tuangalie mfano mwingine:.

Hebu tupate , ambayo itatuwezesha kuamua sababu ya kawaida ya usemi huu:.

Tumepata kanuni ya hesabu kamili. Unahitaji kupata gcd yao na kuiondoa kwenye mabano. Wacha tuunganishe sheria hii kwa kutatua mfano mmoja zaidi.

Tumeangalia sheria ya kugawa sababu ya kawaida kwa coefficients kamili, wacha tuendelee kwenye sehemu ya herufi. Kwanza tunatafuta barua hizo ambazo zimejumuishwa katika monomials zote, na kisha tunaamua shahada kubwa zaidi barua ambayo imejumuishwa katika monomia zote:.

Katika mfano huu kulikuwa na tofauti moja tu ya barua ya kawaida, lakini kunaweza kuwa na kadhaa, kama katika mfano ufuatao:

Wacha tufanye mfano kwa kuongeza idadi ya monomials:

Baada ya kuchukua kipengele cha kawaida, tulibadilisha jumla ya aljebra kuwa bidhaa.

Tuliangalia sheria za kutoa kwa coefficients kamili na vigezo vya herufi kando, lakini mara nyingi unahitaji kuzitumia pamoja ili kutatua mfano. Hebu tuangalie mfano:

Wakati mwingine inaweza kuwa vigumu kuamua ni usemi gani uliobaki kwenye mabano, hebu tuangalie hila rahisi ambayo itawawezesha kutatua tatizo hili haraka.

Sababu ya kawaida inaweza pia kuwa thamani inayotakiwa:

Sababu ya kawaida inaweza kuwa sio nambari tu au monomial, lakini pia usemi wowote, kama vile mlinganyo ufuatao.

Ili kupunguza sehemu hadi kiwango cha chini kabisa cha denominator, unahitaji: 1) kupata kizidishio cha kawaida zaidi cha visehemu vya sehemu ulizopewa, kitakuwa kipunguzo cha kawaida zaidi. 2) tafuta kipengele cha ziada kwa kila sehemu kwa kugawanya denominator mpya kwa kiashiria cha kila sehemu. 3) kuzidisha nambari na denominator ya kila sehemu kwa sababu yake ya ziada.

Mifano. Punguza sehemu zifuatazo hadi kiwango cha chini kabisa cha kawaida chao.

Tunapata kizidishio cha kawaida cha chini kabisa cha madhehebu: LCM(5; 4) = 20, kwa kuwa 20 ndiyo nambari ndogo ambayo inaweza kugawanywa na 5 na 4. Tafuta kwa sehemu ya 1 kipengele cha 4 cha ziada (20). : 5=4). Kwa sehemu ya 2 sababu ya ziada ni 5 (20 : 4=5). Tunazidisha nambari na denominator ya sehemu ya 1 na 4, na nambari na kiashiria cha sehemu ya 2 kwa 5. Tumepunguza sehemu hizi hadi denominator ya chini kabisa ( 20 ).

Denominator ya chini kabisa ya sehemu hizi ni nambari 8, kwani 8 inaweza kugawanywa na 4 na yenyewe. Hakutakuwa na sababu ya ziada kwa sehemu ya 1 (au tunaweza kusema kuwa ni sawa na moja), kwa sehemu ya 2 sababu ya ziada ni 2 (8). : 4=2). Tunazidisha nambari na denominator ya sehemu ya 2 kwa 2. Tumepunguza sehemu hizi hadi denominator ya chini kabisa ( 8 ).

Sehemu hizi haziwezi kupunguzwa.

Wacha tupunguze sehemu ya 1 na 4, na tupunguze sehemu ya 2 na 2. ( tazama mifano kwa ufupisho sehemu za kawaida: Ramani ya tovuti → 5.4.2. Mifano ya kupunguza sehemu za kawaida) Tafuta LOC(16 ; 20)=2 4 · 5=16· 5=80. Kizidishi cha ziada cha sehemu ya 1 ni 5 (80 : 16=5). Sababu ya ziada ya sehemu ya 2 ni 4 (80 : 20=4). Tunazidisha nambari na denominator ya sehemu ya 1 kwa 5, na nambari na kiashiria cha sehemu ya 2 kwa 4. Tumepunguza sehemu hizi hadi nambari ya chini kabisa ya kawaida ( 80 ).

Tunapata dhehebu la chini kabisa la kawaida NCD(5 ; 6 na 15)=NOK(5 ; 6 na 15)=30. Sababu ya ziada kwa sehemu ya 1 ni 6 (30 : 5=6), kipengele cha ziada kwa sehemu ya 2 ni 5 (30 : 6=5), kipengele cha ziada kwa sehemu ya 3 ni 2 (30 : 15=2). Tunazidisha nambari na denominator ya sehemu ya 1 na 6, nambari na denominator ya sehemu ya 2 na 5, nambari na denominator ya sehemu ya 3 kwa 2. Tumepunguza sehemu hizi hadi denominator ya chini kabisa ( 30 ).

Ukurasa wa 1 wa 1 1

Denominator ya sehemu ya hesabu a / b ni nambari b, ambayo inaonyesha saizi ya sehemu za kitengo ambacho sehemu hiyo imeundwa. Denominator ya sehemu ya algebraic A / B inaitwa usemi wa algebra B. Ili kufanya hesabu na sehemu, lazima zipunguzwe hadi kiwango cha chini kabisa cha kawaida.

Utahitaji

• Ili kufanya kazi na sehemu za aljebra na kupata kiashiria cha chini kabisa cha kawaida, unahitaji kujua jinsi ya kuhesabu polynomia.

Maagizo

Hebu tuzingatie kupunguza sehemu mbili za hesabu n/m na s/t hadi kiwango cha chini kabisa cha kawaida, ambapo n, m, s, t ni nambari kamili. Ni wazi kwamba sehemu hizi mbili zinaweza kupunguzwa kwa denominator yoyote inayogawanyika kwa m na t. Lakini wanajaribu kuongoza kwa dhehebu la chini kabisa. Ni sawa na kizidishio kidogo cha kawaida cha madhehebu m na t ya sehemu zilizotolewa. Kizidishio kidogo zaidi (LMK) cha nambari ndicho nambari ndogo zaidi inayoweza kugawanywa na nambari zote zilizotolewa kwa wakati mmoja. Wale. kwa upande wetu, tunahitaji kupata idadi ndogo ya kawaida ya nambari m na t. Inajulikana kama LCM (m, t). Ifuatayo, sehemu hizo huzidishwa na zile zinazolingana: (n/m) * (LCM (m, t) / m), (s/t) * (LCM (m, t) / t).

Wacha tupate dhehebu la chini kabisa la sehemu tatu: 4/5, 7/8, 11/14. Kwanza, hebu tupanue madhehebu 5, 8, 14: 5 = 1 * 5, 8 = 2 * 2 * 2 = 2^3, 14 = 2 * 7. Kisha, hesabu LCM (5, 8, 14) kwa kuzidisha. nambari zote zimejumuishwa katika angalau moja ya upanuzi. LCM (5, 8, 14) = 5 * 2^3 * 7 = 280. Kumbuka kwamba ikiwa sababu hutokea katika upanuzi wa idadi kadhaa (sababu 2 katika upanuzi wa denominators 8 na 14), basi tunachukua sababu shahada kubwa (2 ^ 3 kwa upande wetu).

Kwa hivyo, ya jumla hupatikana. Ni sawa na 280 = 5 * 56 = 8 * 35 = 14 * 20. Hapa tunapata nambari ambazo tunahitaji kuzidisha sehemu na madhehebu yanayolingana ili kuwaleta kwa kiwango cha chini cha kawaida. Tunapata 4/5 = 56 * (4/5) = 224/280, 7/8 = 35 * (7/8) = 245/280, 11/14 = 20 * (11/14) = 220/280.

Kupunguza sehemu za algebraic hadi denominator ya chini kabisa hufanywa kwa mlinganisho na zile za hesabu. Kwa uwazi, hebu tuangalie tatizo kwa kutumia mfano. Acha sehemu mbili (2 * x) / (9 * y^2 + 6 * y + 1) na (x^2 + 1) / (3 * y^2 + 4 * y + 1) zitolewe. Wacha tuangalie madhehebu yote mawili. Kumbuka kwamba denominator ya sehemu ya kwanza ni mraba kamili: 9 * y^2 + 6 * y + 1 = (3 * y + 1)^2. Kwa

>> Hisabati: Kuondoa sababu ya kawaida kwenye mabano

Kabla ya kuanza kusoma sehemu hii, rudi kwa § 15. Hapo tayari tuliangalia mfano ambao ulihitajika kuwasilisha. polynomial kama bidhaa ya polynomial na monomial. Tumegundua kuwa shida hii sio sahihi kila wakati. Ikiwa, hata hivyo, iliwezekana kutunga bidhaa hiyo, basi kwa kawaida wanasema kwamba polynomial inafanywa kwa njia ya kuondolewa kwa jumla kwa sababu ya kawaida kutoka kwa mabano. Hebu tuangalie mifano michache.

Mfano 1. Sababu ya polynomial:

A) 2x + 6y, c) 4a 3 + 6a 2; e) 5a 4 - 10a 3 + 15a 8.
b) a 3 + a 2; d) 12ab 4 - 18a 2 b 3 c;

Suluhisho.
a) 2x + 6y = 2 (x + 3). Kigawanyiko cha kawaida cha mgawo wa masharti ya polynomial kimetolewa kwenye mabano.

b) a 3 + a 2 = a 2 (a + 1). Ikiwa tofauti sawa imejumuishwa katika masharti yote ya polynomial, basi inaweza kuchukuliwa nje ya mabano kwa kiwango sawa na ndogo zaidi ya zilizopo (yaani, chagua ndogo zaidi ya vielelezo vinavyopatikana).

c) Hapa tunatumia mbinu sawa na wakati wa kusuluhisha mifano a) na b): kwa coefficients tunapata kigawanyiko cha kawaida (katika kesi hii nambari 2), kwa anuwai - ndogo zaidi. shahada kutoka kwa zile zinazopatikana (katika kesi hii 2). Tunapata:

4a 3 + 6a 2 = 2a 2 2a + 2a 2 3 = 2a 2 (2a + 3).

d) Kawaida kwa coefficients kamili hujaribu kupata sio tu kigawanyiko cha kawaida, lakini kigawanyiko kikubwa zaidi cha kawaida. Kwa viegemeo 12 na 18, itakuwa nambari 6. Tunakumbuka kuwa kigezo a kimejumuishwa katika masharti yote mawili ya polynomial, na kipeoshi kidogo zaidi kikiwa 1. Tofauti b pia imejumuishwa katika masharti yote mawili ya polynomial, pamoja na kipeo kikuu kidogo kikiwa 3. Hatimaye, kigezo c kinajumuishwa tu katika muhula wa pili wa polynomial haijajumuishwa katika muhula wa kwanza, ambayo ina maana kwamba kutofautiana hii haiwezi kuchukuliwa nje ya mabano kwa kiwango chochote. Kama matokeo, tunayo:

12ab 4 - 18a 2 b 3 c = 6ab 3 2b - 6ab 3 Zas = 6ab 3 (2b - Zas).

e) 5a 4 -10a 3 +15a 8 = 5a 3 (a-2 + Kwa 2).

Kwa kweli, katika mfano huu tulitengeneza algorithm ifuatayo.

Maoni . Katika hali zingine, ni muhimu kuchukua mgawo wa sehemu kama sababu ya jumla.

Kwa mfano:

Mfano 2. Factorize:

X 4 y 3 -2x 3 y 2 + 5x 2.

Suluhisho. Wacha tutumie algorithm iliyoandaliwa.

1) Kigawanyiko kikuu cha kawaida cha coefficients -1, -2 na 5 ni 1.
2) Tofauti x imejumuishwa katika masharti yote ya polynomial na vielelezo 4, 3, 2, kwa mtiririko huo; kwa hivyo, x 2 inaweza kutolewa nje ya mabano.
3) Tofauti y haijajumuishwa katika masharti yote ya polynomial; Hii ina maana kwamba haiwezi kuchukuliwa nje ya mabano.

Hitimisho: x 2 inaweza kutolewa nje ya mabano. Kweli, katika kesi hii inafanya akili zaidi kuweka -x 2 nje ya mabano.

Tunapata:
-x 4 y 3 -2x 3 y 2 + 5x 2 = - x 2 (x 2 y 3 + 2xy 2 - 5).

Mfano 3. Je, inawezekana kugawanya polynomial 5a 4 - 10a 3 + 15a 5 katika monomial 5a 3? Ikiwa ndio, basi tekeleza mgawanyiko.

Suluhisho. Katika mfano 1d) tulipata hiyo

5a 4 - 10a 3 + 15a 8 - 5a 3 (a - 2 + Kwa 2).

Hii inamaanisha kuwa polynomial iliyotolewa inaweza kugawanywa na 5a 3, na mgawo utakuwa - 2 + Kwa 2.

Tuliangalia mifano sawa katika § 18; Tafadhali yaangalie tena, lakini wakati huu kutoka kwa mtazamo wa kuondoa kipengele cha kawaida kwenye mabano.

Kuanzisha polynomial kwa kutoa sababu ya kawaida kutoka kwenye mabano kunahusiana kwa karibu na shughuli mbili ambazo tulisoma katika § 15 na 18 - kuzidisha polynomial kwa monomial na kugawanya polynomial kwa. monomial.

Sasa hebu tupanue mawazo yetu kuhusu kuchukua sababu ya kawaida kutoka kwenye mabano. Jambo ni kwamba wakati mwingine usemi wa algebra inatolewa kwa namna ambayo sababu ya kawaida inaweza kuwa si monomial, lakini jumla ya monomials kadhaa.

Mfano 4. Factorize:

2x(x-2) + 5(x-2) 2 .

Suluhisho. Wacha tuanzishe kigezo kipya y = x - 2. Kisha tunapata:

2x (x - 2) + 5 (x - 2) 2 = 2xy + 5y 2.

Tunakumbuka kuwa kutofautisha y kunaweza kutolewa kwenye mabano:

2xy + 5y 2 - y (2x + 5y). Sasa wacha turudi kwenye nukuu ya zamani:

y(2x + 5y) = (x- 2)(2x + 5(x - 2)) = (x - 2)(2x + 5x-10) = (x-2)(7x:-10).

Katika hali kama hizi, baada ya kupata uzoefu fulani, huwezi kuanzisha tofauti mpya, lakini tumia zifuatazo

2x(x - 2) + 5(x - 2) 2 = (x - 2)(2x + 5(x - 2))= (x - 2)(2x + 5x~ 10) = (x - 2)( 7x - 10).

Upangaji wa mada ya kalenda ya hisabati, video kutoka kwa hisabati mtandaoni, Hisabati shuleni pakua

A. V. Pogorelov, Jiometri kwa darasa la 7-11, Kitabu cha maandishi kwa taasisi za elimu

\(5x+xy\) inaweza kuwakilishwa kama \(x(5+y)\). Hakika haya ni maneno yanayofanana, tunaweza kuthibitisha hili ikiwa tutafungua mabano: \(x(5+y)=x \cdot 5+x \cdot y=5x+xy\). Kama unaweza kuona, kama matokeo tunapata usemi wa asili. Hii ina maana kwamba \(5x+xy\) ni sawa na \(x(5+y)\). Kwa njia, hii ni njia ya kuaminika ya kuangalia usahihi wa mambo ya kawaida - kufungua bracket kusababisha na kulinganisha matokeo na kujieleza awali.

Kanuni kuu ya kuweka mabano:

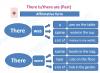
Kwa mfano, katika usemi \(3ab+5bc-abc\) \(b\) pekee ndio unaoweza kutolewa kwenye mabano, kwa sababu ndio pekee uliopo katika maneno yote matatu. Mchakato wa kuchukua mambo ya kawaida kutoka kwa mabano umeonyeshwa kwenye mchoro hapa chini:

Sheria za mabano

Katika hisabati, ni kawaida kuchukua mambo yote ya kawaida mara moja.

Mfano:\(3xy-3xz=3x(y-z)\)
Tafadhali kumbuka kuwa hapa tunaweza kupanua kama hii: \(3(xy-xz)\) au kama hii: \(x(3y-3z)\). Walakini, hizi zitakuwa mtengano usio kamili. C na X lazima ziondolewe.


Wakati mwingine wanachama wa kawaida hawaonekani mara moja.


Mfano:\(10x-15y=2·5·x-3·5·y=5(2x-3y)\)
Katika kesi hii, neno la kawaida (tano) lilifichwa. Walakini, baada ya kupanua \(10\) kama \(2\) ikizidishwa na \(5\), na \(15\) kama \(3\) ikizidishwa na \(5\) - "tulivuta tano kwenye nuru ya Mungu”, baada ya hapo waliweza kuitoa nje ya mabano kwa urahisi.


Ikiwa monomial imeondolewa kabisa, mtu hubakia kutoka kwake.

Mfano: \(5xy+axy-x=x(5y+ay-1)\)
Tunaweka \(x\) nje ya mabano, na monomia ya tatu inajumuisha x tu. Kwa nini mtu anabaki kutoka kwake? Kwa sababu usemi wowote ukizidishwa na moja, hautabadilika. Hiyo ni, \(x\) hii hii inaweza kuwakilishwa kama \(1\cdot x\). Kisha tuna mlolongo ufuatao wa mabadiliko:

\(5xy+axy-\)\(x\) \(=5xy+axy-\)\(1 \cdot x\) \(=\)\(x\) \((5y+ay-\)\ (1\)\()\)

Aidha, hii ndiyo pekee njia sahihi kuondolewa, kwa sababu ikiwa hatutaacha moja, basi tunapofungua mabano hatutarudi kwenye usemi wa asili. Hakika, tukifanya uchimbaji kama huu \(5xy+axy-x=x(5y+ay)\), basi tukipanuliwa tutapata \(x(5y+ay)=5xy+axy\). Mwanachama wa tatu hayupo. Hii ina maana kwamba taarifa kama hiyo si sahihi.

Unaweza kuweka ishara ya kutoa nje ya mabano, na ishara za maneno kwenye mabano zinabadilishwa.


Mfano:\(x-y=-(-x+y)=-(y-x)\)
Kimsingi, hapa tunaweka "minus moja", ambayo inaweza "kuchaguliwa" mbele ya monomial yoyote, hata ikiwa hapakuwa na minus mbele yake. Tunatumia hapa ukweli kwamba mtu anaweza kuandikwa kama \((-1) \cdot (-1)\). Hapa kuna mfano huo huo, ulioelezewa kwa undani:

\(x-y=\)
\(=1·x+(-1)·y=\)
\(=(-1)·(-1)·x+(-1)·y=\)
\(=(-1)·((-1)·x+y)=\)
\(=-(-x+y)=\)
\(-(y-x)\)

Mabano pia yanaweza kuwa sababu ya kawaida.


Mfano:\(3m(n-5)+2(n-5)=(n-5)(3m+2)\)
Mara nyingi tunakutana na hali hii (kuondoa mabano kutoka kwa mabano) wakati wa kuweka alama kwa kutumia njia ya kambi au